Exam 12: Modeling Randomness
Exam 1: Preliminaries: Introduction to Statistical Investigations46 Questions
Exam 2: Significance: How Strong Is the Evidence75 Questions
Exam 3: Generalization: How Broadly Do the Results Apply64 Questions
Exam 4: Estimation: How Large Is the Effect61 Questions
Exam 5: Causation: Can We Say What Caused the Effect30 Questions
Exam 6: Comparing Two Proportions46 Questions
Exam 7: Comparing Two Means46 Questions
Exam 8: Paired Data: One Quantitative Variable48 Questions
Exam 9: Comparing More Than Two Proportions46 Questions
Exam 10: Comparing More Than Two Means28 Questions
Exam 11: Two Quantitative Variables73 Questions
Exam 12: Modeling Randomness129 Questions
Select questions type
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Calculate σX2.
(Short Answer)
4.9/5  (30)
(30)
A tire manufacturer designed a new tread pattern for its all-weather tires. Repeated tests were conducted on cars of approximately the same weight traveling at 60 miles per hour. The tests showed that the new tread pattern enables the cars to stop completely in an average distance of 125 feet with a standard deviation of 6.5 feet and that the stopping distances are approximately normally distributed.
-One car tested had a stopping distance of 140 feet. Calculate the z-score for this observation.
(Short Answer)
4.9/5  (29)
(29)
Which of the following most represents the shape of the distribution of the average number of miles per day put on a typical one of the company's rental car in a year (365 days)? 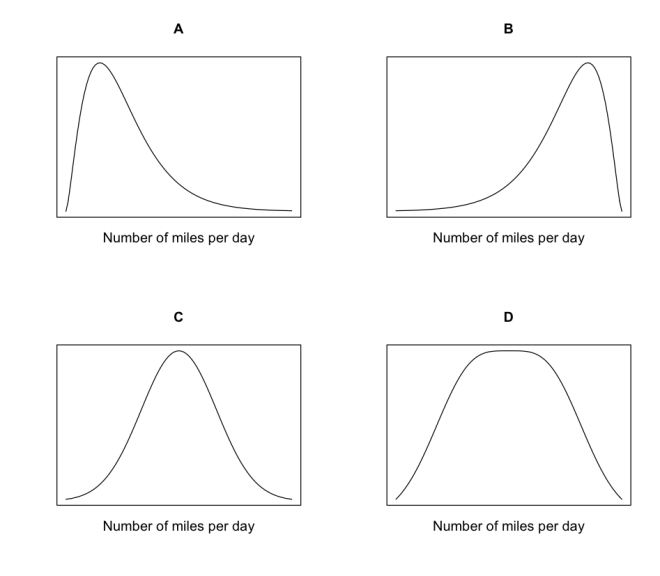
(Short Answer)
4.8/5  (36)
(36)
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-A simulation of this random process was run 1,000 times, assuming the participant did not have ESP, and the number of correct guesses was recorded on each simulation. A bar plot of the results follows. 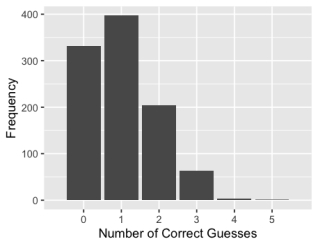 Using the bar plot, estimate the probability of three or more correct guesses.
Using the bar plot, estimate the probability of three or more correct guesses.
(Multiple Choice)
4.9/5  (32)
(32)
An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Calculate the standard deviation of X.
$________
(Short Answer)
4.8/5  (31)
(31)
Assume that events and are mutually exclusive, where and . What is ?
(Multiple Choice)
4.9/5  (38)
(38)
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. The probability distribution function of X is given below.  -Let $D be the expected value of X. Which of the following is a correct interpretation of this value?
-Let $D be the expected value of X. Which of the following is a correct interpretation of this value?
(Multiple Choice)
5.0/5  (35)
(35)
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. From past data, the insurance company has determined that E(X) = $72, and σ_X = $60.
Suppose the insurance company decides to offer a discount to attract new customers. They will pay the new customer $50 for joining, and offer a 5% "cash back" offer for all claims paid. Let Y be the amount in claims (in dollars) for a randomly chosen new customer. Then Y=50+1.05X.
-Find σY2.
(Short Answer)
4.8/5  (36)
(36)
A soft drink company holds a contest in which a prize may be revealed on the inside of the bottle cap. The probability that each bottle cap reveals a prize is 0.26, and winning is independent from one bottle to the next. You plan to keep buying bottles until you win a prize. Let X be the number of bottles you purchase.
-Calculate P(X=5).
(Short Answer)
4.8/5  (30)
(30)
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-How would you write the event that a college student "does not participate in a campus meal program" in probability notation?
(Multiple Choice)
4.8/5  (40)
(40)
The volume in a can of soda is normally distributed with mean 358 mililiters (ml) and standard deviation 6 ml.
-Fill in the two blanks: About 68% of soda cans will contain between
____(1)_____ and _____(2)_____ ml of soda.
(Short Answer)
4.9/5  (34)
(34)
An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Let $D be the expected value of X. Which of the following is a correct interpretation of this value?
(Multiple Choice)
4.8/5  (22)
(22)
A tire manufacturer designed a new tread pattern for its all-weather tires. Repeated tests were conducted on cars of approximately the same weight traveling at 60 miles per hour. The tests showed that the new tread pattern enables the cars to stop completely in an average distance of 125 feet with a standard deviation of 6.5 feet and that the stopping distances are approximately normally distributed.
-Define X as in question 103. Calculate P(X = 0).
(Short Answer)
4.7/5  (34)
(34)
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-What is the appropriate expression for the probability that a randomly chosen college student who lives in a campus residence hall participates in a campus meal program?
(Multiple Choice)
4.7/5  (37)
(37)
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-Based on the simulation results in the bar plot, if someone guessed correctly four times, would you consider this evidence that the person has ESP?
(Multiple Choice)
4.9/5  (41)
(41)
Suppose that 45% of customers at the local farmer's market prefer plastic bags to paper bags, whereas 62% of customers at the local grocery store prefer plastic bags to paper bags. You plan to take a simple random sample of 40 farmer's market customers and 40 grocery story customers and survey their bag preferences. Define p ̂_F-p ̂_G as the difference in sample proportions that prefer plastic bags to paper bags between the two locations (farmer's market - grocery store).
-Can we apply the normal approximation to the distribution of PF-PG?
(Multiple Choice)
4.8/5  (31)
(31)
Suppose X is a random variable with E(X)=5 and σX2=4. Define Y=2X+8.
-Calculate the variance of Y.
(Short Answer)
4.9/5  (38)
(38)
A rental car company has noticed that the distribution of the number of miles customers put on rental cars per day is skewed to the right, with some occasional high outliers. The distribution has a mean of 80 miles and a standard deviation of 50 miles.
-Which of the following most represents the shape of the distribution of the number of miles customers put on rental cars per day? 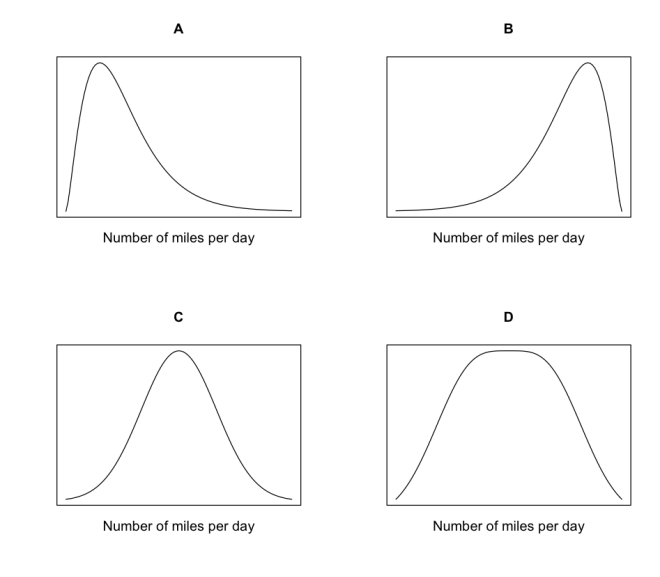
(Short Answer)
4.8/5  (37)
(37)
Based on her past experience, a professor knows that the probability distribution function for X = number of students who come to her office hours on any given Wednesday is given below.  -The expected value of X is 1.85. Interpret this value in the context of the problem.
-The expected value of X is 1.85. Interpret this value in the context of the problem.
(Multiple Choice)
4.7/5  (41)
(41)
Showing 101 - 120 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)