Exam 12: Modeling Randomness
Exam 1: Preliminaries: Introduction to Statistical Investigations46 Questions
Exam 2: Significance: How Strong Is the Evidence75 Questions
Exam 3: Generalization: How Broadly Do the Results Apply64 Questions
Exam 4: Estimation: How Large Is the Effect61 Questions
Exam 5: Causation: Can We Say What Caused the Effect30 Questions
Exam 6: Comparing Two Proportions46 Questions
Exam 7: Comparing Two Means46 Questions
Exam 8: Paired Data: One Quantitative Variable48 Questions
Exam 9: Comparing More Than Two Proportions46 Questions
Exam 10: Comparing More Than Two Means28 Questions
Exam 11: Two Quantitative Variables73 Questions
Exam 12: Modeling Randomness129 Questions
Select questions type
Suppose you roll a six-sided die once. Define events
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Find P(BC).
(Short Answer)
4.8/5  (31)
(31)
Suppose that 70% of the seniors at a large university have taken calculus, and 30% of the seniors have taken physics. Of the seniors who have taken calculus, 40% have taken physics. A student who is a senior at this university is randomly selected. Define the following events.
A = The student has taken calculus
B = The student has taken physics
-Which of the following is true about the events A and B?
(Multiple Choice)
4.9/5  (24)
(24)
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Use the rules for expected value for linear transformations to find σY2.
(Short Answer)
4.8/5  (34)
(34)
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-The ESP test website states: "Keep in mind that your results should only be considered suggestive, because high scores in these tests can be due to chance as well as to actual abilities. Only repeated testing can distinguish between luck and genuine psi abilities." Suppose you take the test five times. How would you simulate the probability of choosing the correct card in at least three of the trials, assuming you do not have ESP?
(Multiple Choice)
5.0/5  (26)
(26)
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Write the probability 0.42 in probability notation.
(Multiple Choice)
4.8/5  (29)
(29)
Math SAT scores for students admitted to University A are bell-shaped with a mean of 520 and a standard deviation of 60. Math SAT scores for students admitted to University B are also bell-shaped, but with a mean of 580 and a standard deviation of 45. Suppose you plan to take a simple random sample of 15 students from University A and 25 students from University B. Let xB-xA be the difference in sample mean math SAT scores between the two samples (B - A).
-What is 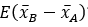 ?
?
(Short Answer)
4.8/5  (32)
(32)
Which of the following variables is a discrete random variable?
(Multiple Choice)
4.9/5  (33)
(33)
Suppose that 70% of the seniors at a large university have taken calculus, and 30% of the seniors have taken physics. Of the seniors who have taken calculus, 40% have taken physics. A student who is a senior at this university is randomly selected. Define the following events.
A = The student has taken calculus
B = The student has taken physics
-Find P(A?B)
(Multiple Choice)
4.9/5  (41)
(41)
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Fill in the probability table below to represent this scenario.

(Essay)
4.9/5  (43)
(43)
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Are the events and independent?
(Multiple Choice)
4.8/5  (39)
(39)
A soft drink company holds a contest in which a prize may be revealed on the inside of the bottle cap. The probability that each bottle cap reveals a prize is 0.39, and winning is independent from one bottle to the next. You buy six bottles. What is the probability that none of the six bottles reveals a prize?
(Multiple Choice)
4.8/5  (35)
(35)
Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events:
A = person has the disease
B = person tests positive on the diagnostic test
-Fill in the tree diagram below to represent this scenario.
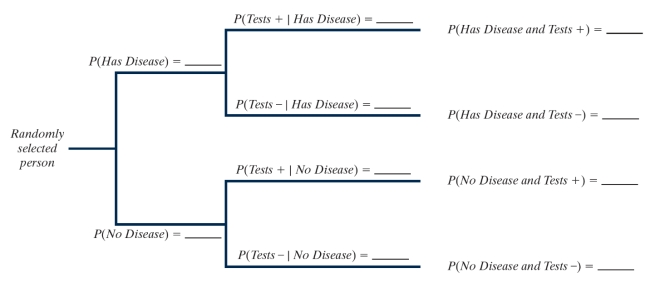
(Essay)
4.8/5  (36)
(36)
Use the Normal Probability Calculator applet to approximate the probability that one of the company's rental cars will average over 85 miles per day.
(Short Answer)
4.9/5  (30)
(30)
Assume that events A and B are independent, where P(A)=0.3 and P(B)=0.6. What is P(A|B)?
(Multiple Choice)
4.8/5  (40)
(40)
A soft drink company holds a contest in which a prize may be revealed on the inside of the bottle cap. The probability that each bottle cap reveals a prize is 0.26, and winning is independent from one bottle to the next. You plan to keep buying bottles until you win a prize. Let X be the number of bottles you purchase.
-What is the distribution of X?
(Multiple Choice)
4.9/5  (33)
(33)
Let X = the average number of miles per day put on a typical one of the company's rental car in a year (365 days). What is E(X)?
(Short Answer)
4.7/5  (34)
(34)
The volume in a can of soda is normally distributed with mean 358 mililiters (ml) and standard deviation 6 ml.
-What is the probability that a six-pack of soda cans have a total volume of at least 2150 ml? Assume the six cans are filled independently.
(Short Answer)
4.8/5  (43)
(43)
According to my neighbor, the probability that the tomato plants she planted last month will actually survive to produce fruit is only 0.6. This means her tomato plants will survive to produce fruit in the next six out of 10 growing seasons.
(True/False)
4.9/5  (25)
(25)
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Use the rules for expected value for linear transformations to find E(Y).
$________
(Short Answer)
4.9/5  (33)
(33)
Showing 81 - 100 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)