Exam 4: Linear Programming: Applications and Solutions
Exam 1: Introduction to Management Science, Modeling, and Excel Spreadsheets33 Questions
Exam 2: Forecasting75 Questions
Exam 3: Linear Programming: Basic Concepts and Graphical Solutions59 Questions
Exam 4: Linear Programming: Applications and Solutions61 Questions
Exam 5: Linear Programming: Sensitivity Analysis, Duality, and Specialized Models55 Questions
Exam 6: Transportation, Assignment, and Transshipment Problems53 Questions
Exam 7: Integer Programming58 Questions
Exam 8: Network Optimization Models61 Questions
Exam 9: Nonlinear Optimization Models60 Questions
Exam 10: Multi-Criteria Models60 Questions
Exam 11: Decision Theory59 Questions
Exam 12: Markov Analysis52 Questions
Exam 13: Waiting Line Models50 Questions
Exam 14: Simulation Cdrom Modules47 Questions
Select questions type
All linear programming formulations with minimize objective function can be converted into an equivalent problem with maximize objective function by simply multiplying the objective function expression by -1 and leaving constraints unchanged.
(True/False)
4.7/5  (35)
(35)
Midwest Money Manger (MMM), an investment firm, has million to invest. They have four choices, namely stocks, bonds, money-markets, and government securities. The respective projected yields are: , and . The respective risk indices are: , and 0.01 . It is assumed that the risk index of a portfolio is equal to the weighted average value of individual index, using the proportion of investment as weights. MMM wants to limit its investment in stocks and bonds to a maximum of of the total investment. Investment in money markets should always be less than or equal to investment in government securities. MMM wants to earn at least in the next year and minimize the risk of its portfolio. Formulate this as a linear program. Specify the decision variables, constraints, and the objective function. Given the following formulation, verify the feasibility of the solution: Invest as follows: Stocks ; Bonds ; Money-market ; Government securities : is feasible. Is it feasible? Is it optimal?
(Essay)
4.9/5  (38)
(38)
If a linear program is unbounded, removing one constraint from the linear program, but keeping all other things unchanged, may make the problem bounded and hence have an optimal solution.
(True/False)
4.8/5  (39)
(39)
A two-variable linear programming problem cannot be solved by the simplex method.
(True/False)
4.8/5  (37)
(37)
A company produces two products A and B. Both can be produced in any of the two machines called old machine and new machine. The following table gives the cost/unit, selling price per unit, maximum daily demand, daily variable cost budget, etc. for the products. The planning horizon is 1 day of 480 working minutes.
 Each machine is available for 480 minutes a day. Daily variable cost budget is . As a production planner, assume that you have the freedom to decide the type and number of products to make and which machine to use, in order to maximize daily net contribution (selling price - variable cost). Formulate this as a linear program. Specify the decision variables, constraints, and the objective function. Solve it using any computer program.
Each machine is available for 480 minutes a day. Daily variable cost budget is . As a production planner, assume that you have the freedom to decide the type and number of products to make and which machine to use, in order to maximize daily net contribution (selling price - variable cost). Formulate this as a linear program. Specify the decision variables, constraints, and the objective function. Solve it using any computer program.
(Essay)
4.7/5  (39)
(39)
If a linear program does not have a feasible solution, adding one more constraint to the linear program, but keeping all other things unchanged, may make the problem feasible.
(True/False)
4.9/5  (34)
(34)
In a linear programming problem with an inequality constraint and an optimal solution, if the inequality constraint is changed to an inequality constraint, all other things remaining the same, the problem may become unbounded.
(True/False)
4.8/5  (44)
(44)
In a linear program, if the constraint simply relates the ratio of constant multiples of two decision variables to another decision variable through , or , then the constraint can always be converted to a linear constraint.
(True/False)
4.9/5  (27)
(27)
XYZ Inc. faces the following data on cost, demand and resource requirnments:
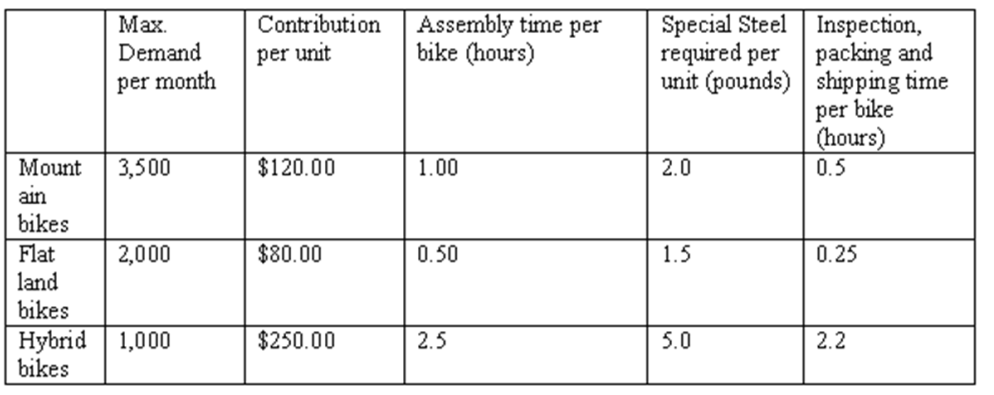 They have a total of 5,000 hours assembly time, and 9,000 hours of inspection, packing, and shipping time available per month. 4,000 pounds of special steel are available in a month. Formulate a linear programming model of this production planning problem so as to maximize the total contribution per month. Solve the problem formulated and report on the optimal solution and its corresponding objective function value.
They have a total of 5,000 hours assembly time, and 9,000 hours of inspection, packing, and shipping time available per month. 4,000 pounds of special steel are available in a month. Formulate a linear programming model of this production planning problem so as to maximize the total contribution per month. Solve the problem formulated and report on the optimal solution and its corresponding objective function value.
(Essay)
4.8/5  (30)
(30)
Graphical simplex is a good alternative to simplex method for all linear programming problems.
(True/False)
4.9/5  (31)
(31)
Midwest Money Manger (MMM), an investment firm, has million to invest. They have four choices, namely stocks, bonds, money-markets, and government securities. The respective projected yields are: , and . The respective risk indices are: , and 0.01 . It is assumed that the risk index of a portfolio is equal to the weighted average value of the individual index, using the proportion of investment as weights. MMM wants to limit its investment in stocks and bonds to a maximum of of the total investment. Investment in money markets should always be less than or equal to investment in government securities. MMM wants its portfolio risk index to be no more than 0.105 and wants to maximize the earnings of its portfolio. Formulate this as a linear program. Specify the decision variables, constraints, and the objective function.
(Essay)
4.9/5  (30)
(30)
A linear programming formulation, which has an optimal solution, cannot become infeasible by the addition of a single constraint.
(True/False)
5.0/5  (33)
(33)
Problem A is a given formulation of a linear program with an optimal solution. Problem B is a formulation obtained by multiplying constraint 1 of Problem A by a positive constant and leaving all other things unchanged. Problems A and B will have
(Multiple Choice)
4.8/5  (33)
(33)
Problem is a given formulation of a linear program with an optimal solution. Problem is a formulation obtained by multiplying constraint 1 of Problem A by a negative constant and leaving all other things unchanged. Problems A and B may have
(Multiple Choice)
5.0/5  (41)
(41)
In using the Solver package to solve a linear programming problem, the decision variables are assigned to the
(Multiple Choice)
5.0/5  (42)
(42)
If a linear program is unbounded, adding one more constraint to the linear program, but keeping all other things unchanged, may make the problem bounded and hence have an optimal solution.
(True/False)
4.8/5  (34)
(34)
A linear programming formulation, which has a unique optimal solution, cannot have multiple optimal solutions by the addition of a single constraint.
(True/False)
4.9/5  (35)
(35)
In formulating a coffee blending problem where there are three types of coffee beans, the objective is to find a recipe to make 1 pound of blended coffee that satisfies a set of properties at the least cost. The decision variables are , and , representing pounds (actually fractional pounds) of coffee beans used per pound of blended coffee. One of the constraints of the problem will be
(Multiple Choice)
4.8/5  (33)
(33)
In a linear program, if a constraint is of the equality type (=), then solutions that make the constraint will also be allowed (that is, these solutions will also be feasible).
(True/False)
4.8/5  (42)
(42)
A linear programming formulation, which is unbounded, cannot have a feasible solution.
(True/False)
4.8/5  (36)
(36)
Showing 21 - 40 of 61
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)