Exam 12: Markov Analysis
Exam 1: Introduction to Management Science, Modeling, and Excel Spreadsheets33 Questions
Exam 2: Forecasting75 Questions
Exam 3: Linear Programming: Basic Concepts and Graphical Solutions59 Questions
Exam 4: Linear Programming: Applications and Solutions61 Questions
Exam 5: Linear Programming: Sensitivity Analysis, Duality, and Specialized Models55 Questions
Exam 6: Transportation, Assignment, and Transshipment Problems53 Questions
Exam 7: Integer Programming58 Questions
Exam 8: Network Optimization Models61 Questions
Exam 9: Nonlinear Optimization Models60 Questions
Exam 10: Multi-Criteria Models60 Questions
Exam 11: Decision Theory59 Questions
Exam 12: Markov Analysis52 Questions
Exam 13: Waiting Line Models50 Questions
Exam 14: Simulation Cdrom Modules47 Questions
Select questions type
A transient state in a Markov chain is one in which the system cannot stay in for the long run.
(True/False)
4.8/5  (32)
(32)
Judy Jones purchases groceries and pop exactly once each week on Sunday evenings. She buys either Coke or Pepsi only and switches from Coke to Pepsi and vice-versa somewhat regularly. Her purchasing behavior of these two drinks is modeled as a Markov system. Let the transition matrix be:
 If in Week \#7, Judy has purchased Coke, what is the probability that she would purchase Pepsi in Week ?
If in Week \#7, Judy has purchased Coke, what is the probability that she would purchase Pepsi in Week ?
(Multiple Choice)
4.8/5  (39)
(39)
Judy Jones purchases groceries and pop exactly once each week on Sunday evenings. She buys either Coke or Pepsi only and switches from Coke to Pepsi and vice-versa somewhat regularly. Her purchasing behavior of these two drinks is modeled as a Markov system. Let the transition matrix be:
 If in Week\#7, Judy is equally likely to be purchasing Coke or Pepsi (0.5 each), what is the probability that she would purchase Pepsi in Week \#8?
If in Week\#7, Judy is equally likely to be purchasing Coke or Pepsi (0.5 each), what is the probability that she would purchase Pepsi in Week \#8?
(Multiple Choice)
4.8/5  (34)
(34)
XYZ Inc. hires only retired people for its greeter's job. They always start on January 1 and are considered for promotion every January 1st thereafter. On every January 1st, any existing greeter (state G) those who were greeters last year - may be retired (state R), may be dead (sate D), may continue as a greeter (state G), or may be promoted as greeter -in-chief (state GIC). Persons in state GIC may continue in it or move to states D or R in one year. The following is the transition matrix. As per this matrix, more greeters will eventually retire from service as compared to the number who eventually die while in service.

(True/False)
4.9/5  (41)
(41)
Newsweek and Time are two competing weeklies, each of which tries to keep their readership while trying to get the other's readers to switch. Among all the households holding yearly subscription to Newsweek or Time but not both, let and denote the states that a household is a current Newsweek or Time subscriber, respectively. The probabilities of switching from one state to the other after one transition (when they renew) are given by the tree diagram. (For simplicity, it may be assumed that all annual subscriptions expire on December 31st of the year and are renewed by all of them for one or the other but not both magazines for one year.) If the current number of households subscribing for Newsweek and Time is respectively 2000 and 4000, what would be the number of subscribers to Newsweek in the steady state, that is after very many renewals?
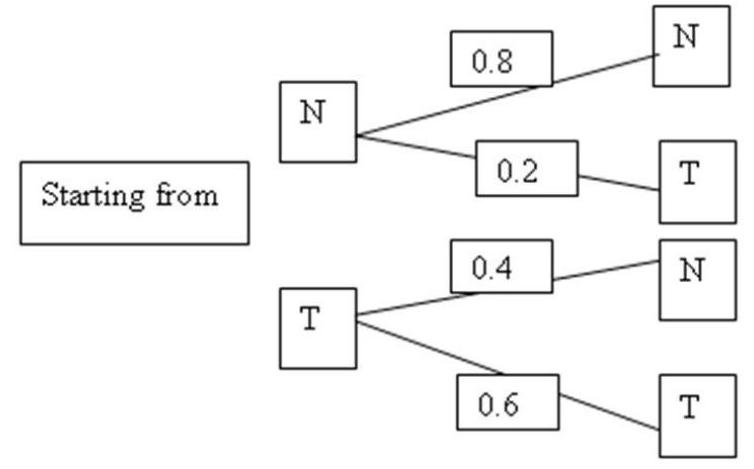
(Multiple Choice)
4.9/5  (40)
(40)
Judy Jones purchases groceries and pop exactly once each week on Sunday evenings. She buys either Coke or Pepsi only and switches from Coke to Pepsi and vice-versa somewhat regularly. Her purchasing behavior of these two drinks is modeled as a Markov system. Let the transition matrix be:
 If in Week \#7, Judy has purchased Coke, what is the probability that she would purchase Pepsi in Week ?
If in Week \#7, Judy has purchased Coke, what is the probability that she would purchase Pepsi in Week ?
(Multiple Choice)
4.8/5  (29)
(29)
If matrix is multiplied by matrix - then the number of rows in should equal the number of columns in B.
(True/False)
4.9/5  (38)
(38)
Markov Analysis has many business applications, such as accounts receivables analysis and machine maintenance.
(True/False)
4.9/5  (36)
(36)
Short term behavior of a Markov system is determined by its transition probability matrix, while the long term behavior is dependent on the starting state of the system.
(True/False)
4.9/5  (44)
(44)
Jim Cramer, a stock analyst, models the movement of the closing price in NYSE of the stock WidgetsR-Us Inc. (symbol: WRU) as a Markov chain with a transition time of 1 day. There are two states in this Markov system-State A, the closing price increased or stayed the same from the previous day and State , the closing price decreased from the previous day. Suppose that the system is on State B as at the end of today, what is the probability that it will be in State B after two trading days (48 hours)?
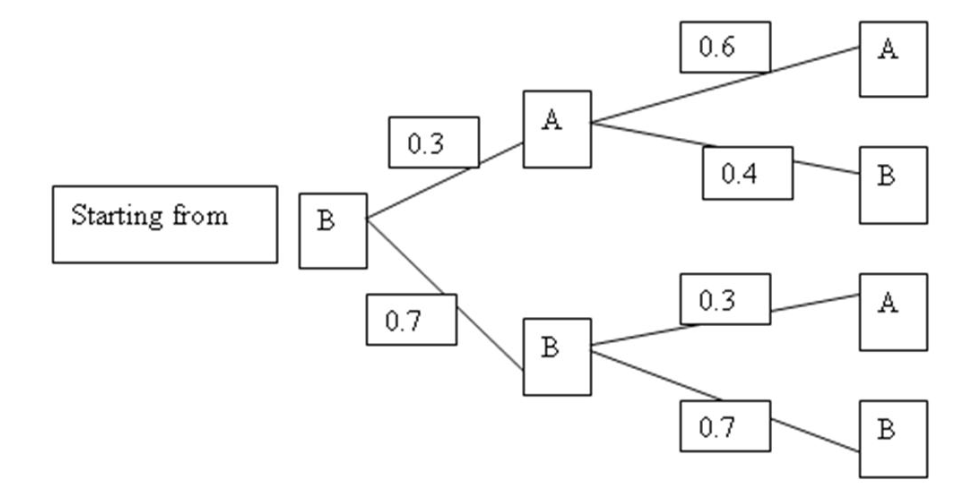
(Multiple Choice)
4.7/5  (44)
(44)
Showing 41 - 52 of 52
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)