Exam 6: Applications of Integration
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Determine the area of the surface generated when the curve is revolved about the indicated axis.
-x = 3 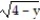 , for 0 y
, for 0 y  ; about the y-axis
; about the y-axis
(Multiple Choice)
4.8/5  (42)
(42)
Find the volume of the described solid.
-The solid lies between planes perpendicular to the x-axis at x = /6 to x = /2. The cross sections perpendicular to the x-axis are circular disks with diameters running from the curve  to the curve
to the curve 
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by x =  , x = 0, y = 1, y = 5
, x = 0, y = 1, y = 5
(Multiple Choice)
4.8/5  (38)
(38)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the 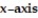 -y = 5cos x, y = 0, x = -0.5, x = 0.5
-y = 5cos x, y = 0, x = -0.5, x = 0.5
(Multiple Choice)
4.8/5  (47)
(47)
Solve the problem.
-Find a curve through the point ( -6, 1) whose length integral, 1 y 2, is L = 
(Multiple Choice)
5.0/5  (29)
(29)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the x-axis 

(Multiple Choice)
4.7/5  (30)
(30)
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated axis.
-About the x-axis

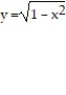
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-The lower edge of a dam is defined by the parabola (see figure). Use a coordinate system with y = 0 at the bottom of the dam to determine the total force on the dam. Lengths are measured in meters. 
(Multiple Choice)
4.8/5  (44)
(44)
Find the area enclosed by the given curves.
-Find the area between the curves y = ln x and y = ln 2x from x = 1 to x = 5.
(Multiple Choice)
4.7/5  (31)
(31)
Set up an integral for the length of the curve.
-y = 8 cos x, 0 x
(Multiple Choice)
4.7/5  (33)
(33)
Find the area enclosed by the given curves.
-Find the area of the region in the first quadrant bounded on the left by the line y =  and on the right by the curves y =
and on the right by the curves y =  x and y =
x and y =  x. (Round to four decimal places.)
x. (Round to four decimal places.)
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-A diving pool that is 5 m deep and full of water has a viewing window on one of its vertical walls. Find the force on a circular window, with a radius of 0.5 m, tangent to the bottom of the pool. Round to three decimal places when appropriate.
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-A heavy-duty shock absorber is compressed 2 cm from its equilibrium position by a mass of 600 kg. How much work is required to compress the shock absorber 5 cm from its equilibrium position? (A mass of 600 kg exerts a force (in N) of 600g, where g 9.8 m/  .)
.)
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-The hemispherical bowl of radius 5 contains water to a depth 2. Find the volume of water in the bowl.
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the 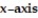 -y = 3cos ( x), y = 3, x = -0.5, x = 0.5
-y = 3cos ( x), y = 3, x = -0.5, x = 0.5
(Multiple Choice)
4.9/5  (46)
(46)
Find the volume of the solid generated by revolving the region about the given axis. Use the shell or washer method.
-The region bounded by y = 7  , y = 7, and x = 0 about the y-axis
, y = 7, and x = 0 about the y-axis
(Multiple Choice)
4.8/5  (39)
(39)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves about the given lines.
-y = 4x, y = 0, x = 2; revolve about the line x = -3
(Multiple Choice)
4.9/5  (46)
(46)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the 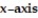 -y = sec x, y = tan x, x = 0, x =
-y = sec x, y = tan x, x = 0, x = 
(Multiple Choice)
4.9/5  (40)
(40)
Showing 21 - 40 of 211
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)