Exam 6: Applications of Integration
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the x-axis.
-x = 3 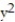 , x = - 3y, y = 3
, x = - 3y, y = 3
(Multiple Choice)
4.8/5  (31)
(31)
Find the volume of the described solid.
-The solid lies between planes perpendicular to the x-axis at x = - 2 and x = 2. The cross sections perpendicular to the x-axis are circular disks whose diameters run from the parabola y = 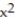 to the parabola y = 8 -
to the parabola y = 8 - 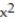 .
.
(Multiple Choice)
4.8/5  (41)
(41)
Use a calculator to approximate the area of the surface generated when the given curve is revolved about the x-axis. Round to two decimal places when necessary.
-y = sinx on 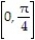
(Multiple Choice)
4.7/5  (39)
(39)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the x-axis.
-y = 2x, y = 4x, y = 2
(Multiple Choice)
4.9/5  (41)
(41)
Find the volume of the described solid.
-The solid lies between planes perpendicular to the x-axis at x = - 3 and x = 3. The cross sections perpendicular to the x-axis are semicircles whose diameters run from 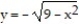 to
to 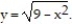
(Multiple Choice)
4.9/5  (45)
(45)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the x-axis.
-y = 7 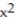 , y = 7
, y = 7 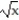
(Multiple Choice)
4.9/5  (39)
(39)
Find the area of the surface generated when the given curve is revolved about the x-axis.
-y = 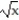 on
on 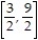
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-Given the acceleration, initial velocity, and initial position of a body moving along a coordinate line at time t, find the body's position at time t. a = 20 cos 5t, v(0) = 8, s(0) = 12
(Multiple Choice)
4.9/5  (33)
(33)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and lines about the x-axis.
-x = 6 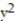 , x = 6
, x = 6 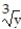
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-A water tank is formed by revolving the curve y = 6 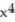 about the y-axis. Find the volume of water in the tank as a function of the water depth, y.
about the y-axis. Find the volume of water in the tank as a function of the water depth, y.
(Multiple Choice)
4.9/5  (36)
(36)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves about the given lines.
-y = 5x, y = 0, x = 4; revolve about the x-axis
(Multiple Choice)
4.7/5  (47)
(47)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by x = 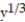 , x = 0, y = 27
, x = 0, y = 27
(Multiple Choice)
4.8/5  (32)
(32)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the x-axis 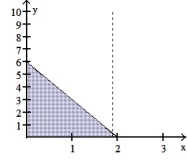
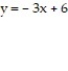
(Multiple Choice)
4.8/5  (44)
(44)
Find the area of the surface generated when the given curve is revolved about the x-axis.
-y = 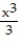 +
+ 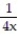 on
on 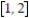
(Multiple Choice)
5.0/5  (38)
(38)
Solve the problem.
-A water trough has a semicircular cross section with a radius of 0.5 m and a length of 4 m (see figure). How much work is required to pump water out of the trough when it is full? Round to two decimal places when appropriate. 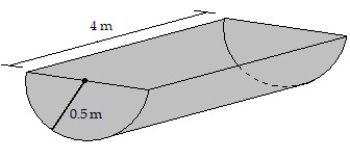
(Multiple Choice)
4.8/5  (39)
(39)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the x-axis 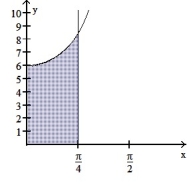

(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-A square plate 3 m on a side is placed on a vertical wall 3 m below the surface of a pool filled with water. On which plate in the figure is the force greater? Try to anticipate the answer and then compute the force on each plate. Round to three decimal places when appropriate. 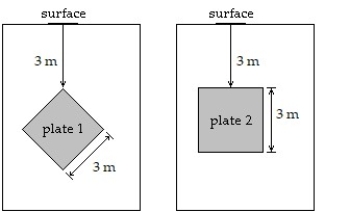
(Multiple Choice)
4.8/5  (38)
(38)
Showing 101 - 120 of 211
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)