Exam 13: Vectors and the Geometry of Space
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Find the angle between u and v in radians.
-u = -2i + 8j - 8k, v = 8i + 4j - 5k
(Multiple Choice)
4.9/5  (38)
(38)
Find the angle between u and v in radians.
-u = -10j and v = 6i - 8k
(Multiple Choice)
4.9/5  (36)
(36)
Identify the quadric surface by name. Find and describe the xy-, xz-, and yz-traces, when they exist.
-16 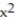 - 16
- 16 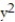 - z = 0
- z = 0
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-A ramp leading to the entrance of a building is inclined upward at an angle of 6°. A suitcase is to be pulled up the ramp by a handle that makes an angle of 34° with the horizontal. How much force must be applied in the direction of the handle so that the component of the force parallel to the ramp is 50 lbs.?
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-A bullet is fired with a muzzle velocity of 1489 ft/sec from a gun aimed at an angle of 12° above the horizontal. Find the horizontal component of the velocity.
(Multiple Choice)
4.7/5  (40)
(40)
Solve the problem.
-Find the work done by a force of 19i (newtons) in moving an object along a line from the origin to the point 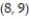 (distance in meters).
(distance in meters).
(Multiple Choice)
4.8/5  (35)
(35)
Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v.
-u = - 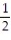 i +
i + 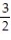 j + k, v = i + j + 2k
j + k, v = i + j + 2k
(Multiple Choice)
4.8/5  (27)
(27)
Express the vector in the form ai + bj + ck.
-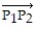 if
if 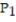 is the point ( 3, 6, -4) and
is the point ( 3, 6, -4) and 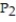 is the point ( 5, 3, -8)
is the point ( 5, 3, -8)
(Multiple Choice)
4.8/5  (42)
(42)
Identify the type of surface represented by the given equation.
-x = -10 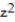 , no limit on y
, no limit on y
(Multiple Choice)
4.8/5  (34)
(34)
Find the corresponding position vector.
-Define the points P = ( -10, -6) and Q = ( -2, 5). Find the position vector corresponding to 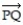 .
.
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-For the vectors u and v with magnitudes 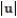 = 7 and
= 7 and 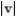 = 8, find the angle between u and v which makes
= 8, find the angle between u and v which makes 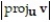 = 5
= 5
(Multiple Choice)
4.8/5  (39)
(39)
Showing 21 - 40 of 131
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)