Exam 13: Vectors and the Geometry of Space
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v.
-u = 2i + 2j - k, v = -i + k
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-For the triangle with vertices located at A( 3, 3, 5), B( 4, 2, 2), and C(1, 1, 1) , find a vector from vertex C to the midpoint of side AB.
(Multiple Choice)
4.8/5  (40)
(40)
Write the equation for the plane.
-The plane passing through the points (1, 2, 6), (-1, 4, 0), and (3, 1, 5).
(Multiple Choice)
4.8/5  (45)
(45)
Determine whether the pairs of lines are parallel, intersect at a single point, or are skew. If the lines are parallel, determine whether they are the same line (and thus intersect at all points). If the lines intersect at a single point, determine the point of intersection.
-r = (3, 1, 4) + t(-1, 6, -2); R = (-6, 55, -14) + t(5, -30, 10)
(Multiple Choice)
4.9/5  (39)
(39)
Express the vector in the form ai + bj + ck.
-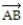 if A is the point ( -4, -8, -5) and B is the point ( 1, -15, -2)
if A is the point ( -4, -8, -5) and B is the point ( 1, -15, -2)
(Multiple Choice)
4.8/5  (27)
(27)
Find the angle between u and v in radians.
-u = -2i - 2j, v = 4i + 9j + 8k
(Multiple Choice)
4.8/5  (41)
(41)
Use a calculator to find the acute angle between the planes to the nearest thousandth of a radian.
-4x - 3y - 5z = 7 and- 8x + 2y - 10z = -9
(Multiple Choice)
4.8/5  (31)
(31)
Find an equation for the sphere with the given center and radius.
-Center (-2, 0, 0), radius = 4
(Multiple Choice)
4.8/5  (31)
(31)
Find the magnitude of u × v and the unit vector parallel to u × v in the direction of u × v.
-u = -3i - 2j - 3k, v = 6i + 4j + 6k
(Multiple Choice)
4.9/5  (37)
(37)
Find the triple scalar product (u x v) ∙ w of the given vectors.
-u = 2i - 4j + 3k; v = -5i - 7j + 8k; w = 9i - 2j + 4k
(Multiple Choice)
5.0/5  (34)
(34)
Give a geometric description of the set of points whose coordinates satisfy the given conditions.
-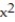 +
+ 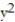 +
+ 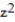 > 1
> 1
(Multiple Choice)
4.7/5  (40)
(40)
Solve the problem.
-Find the magnitude of the torque in foot-pounds at point P for the following lever: 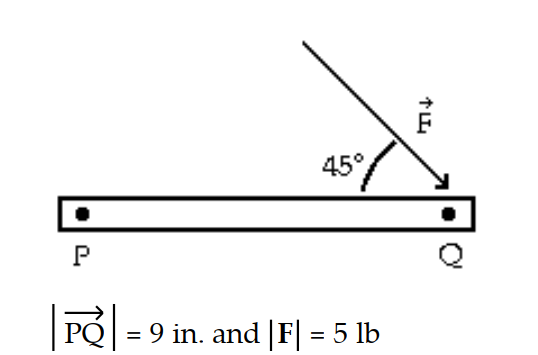
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-An airplane is flying in the direction 50° west of north at 817 km/hr. Find the component form of the velocity of the airplane, assuming that the positive x-axis represents due east and the positive y-axis represents due north.
(Multiple Choice)
4.9/5  (29)
(29)
Use a calculator to find the acute angle between the planes to the nearest thousandth of a radian.
--3x - 2y - 10z = 1 and 6x + 8y - 10z = 9
(Multiple Choice)
4.9/5  (39)
(39)
Find an equation for the sphere with the given center and radius.
-Center (0, -10, -7), radius = 5
(Multiple Choice)
4.8/5  (34)
(34)
Find an equation for the sphere with the given center and radius.
-Center (-8, 10, 0), radius = 5
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-A bird flies from its nest 4 km in the direction 4° north of east, where it stops to rest on a tree. It then flies 7 km in the direction 4° south of west and lands atop a telephone pole. With an xy-coordinate system where the origin is the bird's nest, the x-axis points east, and the y-axis points north, at what point is the telephone pole located?
(Multiple Choice)
4.8/5  (45)
(45)
Showing 81 - 100 of 131
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)