Exam 12: Parametric and Polar Curves
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Find the area of the specified region.
-Inside the cardioid r = (1 + sin ), > 0
(Multiple Choice)
4.8/5  (38)
(38)
Find the area of the specified region.
-Inside the six-leaved rose 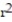 = 8 cos 3
= 8 cos 3
(Multiple Choice)
4.9/5  (44)
(44)
Find a parametrization for the curve.
-The line segment with endpoints ( -8, -7) and ( 0, -12)
(Short Answer)
4.7/5  (35)
(35)
Find the standard-form equation of the hyperbola centered at the origin which satisfies the given conditions.
-Foci at ( 0, -10), ( 0, 10); asymptotes: y =  x, y = -
x, y = -  x
x
(Multiple Choice)
4.8/5  (34)
(34)
Calculate the arc length of the indicated portion of the curve r(t).
-r(t) = ( 7 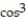 2t)j + ( 7
2t)j + ( 7 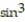 2t)k;
2t)k; 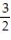 t
t 
(Multiple Choice)
4.8/5  (31)
(31)
Find a parametrization for the curve.
-The upper half of the parabola x + 3 = 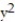
(Short Answer)
4.7/5  (35)
(35)
Replace the polar equation with an equivalent Cartesian equation.
-r cos = 13
(Multiple Choice)
4.9/5  (33)
(33)
Find the standard-form equation of the ellipse centered at the origin and satisfying the given conditions.
-An ellipse with intercepts (±2, 0) and (0, ±5)
(Multiple Choice)
5.0/5  (31)
(31)
Find the standard-form equation of the ellipse centered at the origin and satisfying the given conditions.
-An ellipse with vertices (0, ±8) and foci (0, ±4)
(Multiple Choice)
4.9/5  (36)
(36)
Find the area of the specified region.
-Inside the circle r = 7 and to the right of the line r = 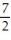 sec
sec
(Multiple Choice)
4.8/5  (35)
(35)
Find the area of the specified region.
-Inside the three-leaved rose r = 6 cos 3
(Multiple Choice)
4.8/5  (41)
(41)
Graph the parabola or ellipse. Include the directrix that corresponds to the focus at the origin.
-r = 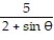
(Multiple Choice)
5.0/5  (26)
(26)
Showing 61 - 80 of 169
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)