Exam 5: Series Solutions of Second-Order Linear Equations
Exam 1: Introduction28 Questions
Exam 2: First-Order Differential Equations73 Questions
Exam 3: Second-Order Linear Differential Equations119 Questions
Exam 4: Higher-Order Linear Differential Equations54 Questions
Exam 5: Series Solutions of Second-Order Linear Equations81 Questions
Exam 6: The Laplace Transform57 Questions
Exam 7: Systems of First-Order Linear Equations97 Questions
Exam 8: Numerical Methods63 Questions
Exam 9: Nonlinear Differential Equations and Stability76 Questions
Exam 10: Partial Differential Equations and Fourier Series44 Questions
Exam 11: Boundary Value Problems and Sturm-Liouville Theory19 Questions
Select questions type
Which of the following pairs forms a fundamental set of solutions of the Cauchy Euler differential equation 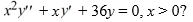 .
.
(Multiple Choice)
4.8/5  (43)
(43)
Consider the second-order differential equation 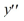 - 19x2 y = 0.
Assume a solution of this equation can be represented as a power series
- 19x2 y = 0.
Assume a solution of this equation can be represented as a power series 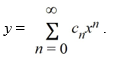 Write down the first four nonzero terms of the power series solution.
y(x) ≈ ________
Write down the first four nonzero terms of the power series solution.
y(x) ≈ ________
(Essay)
4.9/5  (49)
(49)
Consider the first-order differential equation 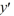 - 7y = 0.
Assume a solution of this equation can be represented as a power series
- 7y = 0.
Assume a solution of this equation can be represented as a power series 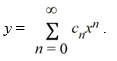 Which of these elementary functions is equal to the power series representation of the solution?
Which of these elementary functions is equal to the power series representation of the solution?
(Multiple Choice)
4.9/5  (35)
(35)
Consider the Bessel equation of order 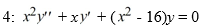 .
Suppose the method of Frobenius is used to determine a power series solution of the form
.
Suppose the method of Frobenius is used to determine a power series solution of the form 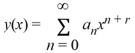 .
Of this differential equation. Assume a0 0.
Which of these is the explicit formula for the coefficients corresponding to the positive root of the indicial equation?
.
Of this differential equation. Assume a0 0.
Which of these is the explicit formula for the coefficients corresponding to the positive root of the indicial equation?
(Multiple Choice)
4.8/5  (28)
(28)
Which of the following pairs forms a fundamental set of solutions of the Cauchy Euler differential equation 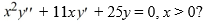 .
.
(Multiple Choice)
4.8/5  (33)
(33)
Consider the first-order differential equation 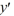 - 5y = 0.
Assume a solution of this equation can be represented as a power series
- 5y = 0.
Assume a solution of this equation can be represented as a power series 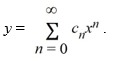 What is the recurrence relation for the coefficients Cn? Assume that C0 is known
What is the recurrence relation for the coefficients Cn? Assume that C0 is known
(Multiple Choice)
4.8/5  (39)
(39)
Find the general solution of the Cauchy Euler differential equation 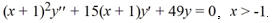 .
.
(Multiple Choice)
4.9/5  (39)
(39)
Consider the Legendre equation: 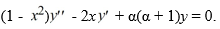 .
Which of these statements is true?
.
Which of these statements is true?
(Multiple Choice)
4.9/5  (33)
(33)
Consider the second-order differential equation 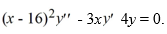 .
Which of these statements is true?
.
Which of these statements is true?
(Multiple Choice)
4.9/5  (30)
(30)
Consider the second-order differential equation 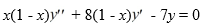 .
Write the differential equation in the form
.
Write the differential equation in the form 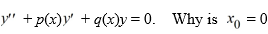 . a regular singular point for this equation?
. a regular singular point for this equation?
(Multiple Choice)
5.0/5  (42)
(42)
Consider the second-order differential equation 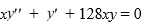 .
Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series
.
Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series 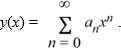 Assume a0 0.
Assuming that a0 = 1, one solution of the given differential equation is
Assume a0 0.
Assuming that a0 = 1, one solution of the given differential equation is 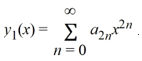 Differentiating as needed, which of these relationships is correct?
Differentiating as needed, which of these relationships is correct?
(Multiple Choice)
4.7/5  (43)
(43)
Consider the second-order differential equation: 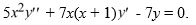 .
Why is C0 = 0 a regular singular point?
.
Why is C0 = 0 a regular singular point?
(Multiple Choice)
4.9/5  (41)
(41)
Consider the first-order differential equation 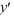 . - 7xy = 0.
Assume a solution of this equation can be represented as a power series
. - 7xy = 0.
Assume a solution of this equation can be represented as a power series 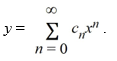 .
What is the recurrence relation for the coefficients Cn ? Assume that C0 is known.
.
What is the recurrence relation for the coefficients Cn ? Assume that C0 is known.
(Multiple Choice)
4.9/5  (27)
(27)
Consider the second-order differential equation: 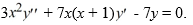 .
Write out the first three terms of the solution corresponding to the positive root of the indicial equation.
Y1 (x) ≈ ________
.
Write out the first three terms of the solution corresponding to the positive root of the indicial equation.
Y1 (x) ≈ ________
(Essay)
4.9/5  (37)
(37)
What is the Taylor series expansion for f(x) = 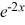 about x = 0?
about x = 0?
(Multiple Choice)
5.0/5  (36)
(36)
Consider the second-order differential equation 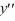 + 100y = 0.
Assume a solution of this equation can be represented as a power series
+ 100y = 0.
Assume a solution of this equation can be represented as a power series 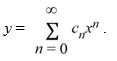 Assume the solution of the given differential equation is written as
Assume the solution of the given differential equation is written as
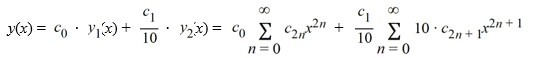 Identify elementary functions for y1 (x) and y2 (x).
y1 (x) = ________
y2 (x) = ________
Identify elementary functions for y1 (x) and y2 (x).
y1 (x) = ________
y2 (x) = ________
(Essay)
4.9/5  (34)
(34)
Consider the second-order differential equation 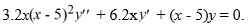 .
Which of these statements is true?
.
Which of these statements is true?
(Multiple Choice)
4.9/5  (36)
(36)
Consider the second-order differential equation 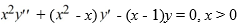 .
Using the method of Frobenius, which of these is the general solution of this differential equation? Assume
.
Using the method of Frobenius, which of these is the general solution of this differential equation? Assume 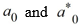 are arbitrary real constants.
are arbitrary real constants.
(Multiple Choice)
4.7/5  (34)
(34)
Showing 41 - 60 of 81
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)