Exam 9: Logarithmic and Exponential Functions
Exam 1: Review of Real Numbers152 Questions
Exam 2: Linear and Absolute Value Equations and Inequalities334 Questions
Exam 3: Graphing Linear Equations353 Questions
Exam 4: Systems of Equations204 Questions
Exam 5: Exponents, Polynomials, and Factoring Polynomials453 Questions
Exam 6: Rational Expressions and Equations249 Questions
Exam 7: Radical Expressions and Equations361 Questions
Exam 8: Quadratic Equations270 Questions
Exam 9: Logarithmic and Exponential Functions404 Questions
Exam 10: Conic Sections122 Questions
Exam 11: Sequences, Series, and the Binomial Theorem154 Questions
Select questions type
Graph. State the domain, range, and vertical asymptote of the function
-
(Multiple Choice)
4.9/5  (52)
(52)
Find all intercepts for the given function. Round to the nearest tenth if necessary.
-
(Multiple Choice)
4.8/5  (31)
(31)
Find the missing number. Round to the nearest hundredth if necessary.
-
(Multiple Choice)
4.9/5  (33)
(33)
Rewrite as the sum of two or more logarithms using the product rule for logarithms. A ssume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (33)
(33)
Rew rite as a single logarithm. A ssume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (34)
(34)
Graph. State the domain, range, and horizontal asymptote of the function
-
(Multiple Choice)
4.9/5  (33)
(33)
Graph a one-to-one function f(x) that meets the given criteria.
- is a quadratic function, the domain of is restricted to , and .
(Multiple Choice)
4.9/5  (41)
(41)
Find the specified domain
-For and , what is the domain of ?
(Multiple Choice)
4.8/5  (28)
(28)
For the given graph of a one-to-one function f(x), graph its inverse functionf-1(x) using a dashed line
-
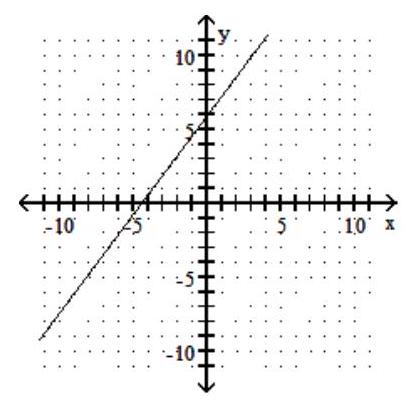
(Multiple Choice)
4.8/5  (37)
(37)
Rewrite using the pow er and product rules. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (31)
(31)
Expand. A ssume that all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (35)
(35)
For the given function , find and graph the function and its inverse.
-
(Multiple Choice)
4.9/5  (31)
(31)
Graph f(x). State the domain, range, and horizontal asymptote of the function
-
(Multiple Choice)
4.8/5  (33)
(33)
Graph f(x). State the domain, range, and horizontal asymptote of the function
-
(Multiple Choice)
4.8/5  (40)
(40)
Showing 61 - 80 of 404
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)