Exam 9: Logarithmic and Exponential Functions
Exam 1: Review of Real Numbers152 Questions
Exam 2: Linear and Absolute Value Equations and Inequalities334 Questions
Exam 3: Graphing Linear Equations353 Questions
Exam 4: Systems of Equations204 Questions
Exam 5: Exponents, Polynomials, and Factoring Polynomials453 Questions
Exam 6: Rational Expressions and Equations249 Questions
Exam 7: Radical Expressions and Equations361 Questions
Exam 8: Quadratic Equations270 Questions
Exam 9: Logarithmic and Exponential Functions404 Questions
Exam 10: Conic Sections122 Questions
Exam 11: Sequences, Series, and the Binomial Theorem154 Questions
Select questions type
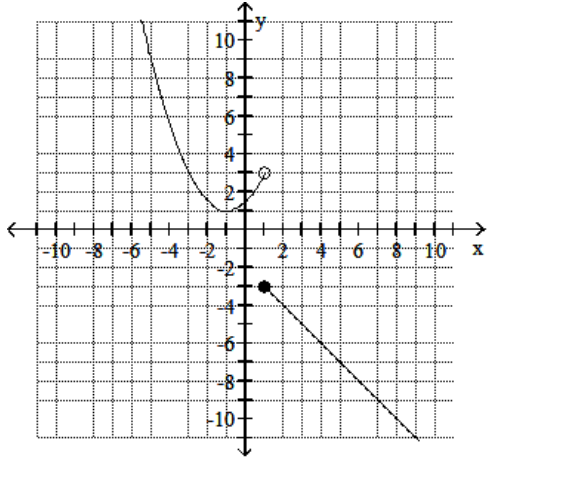
Use the graph of the piecewise function f(x) to find the following
-
(Multiple Choice)
4.9/5  (32)
(32)
Evaluate. Round to the nearest thousandth, if necessary.
-
(Multiple Choice)
4.8/5  (35)
(35)
Express as a composition of two functions and : (f . A nsw ers may vary. Choose the possible answer.
-
(Multiple Choice)
5.0/5  (31)
(31)
Solve the problem.
-Approximately one fourth of all glass bottles distributed will be recycled each year. A beverage company distributes 330,000 bottles. The number still in use after years is given by the function
After how many years will 4000 bottles still be in use? Round your answer to the nearest tenth.
(Multiple Choice)
4.7/5  (32)
(32)
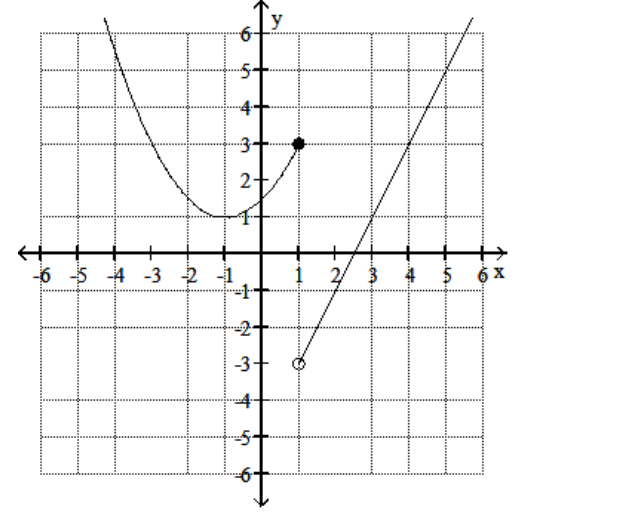
Use the graph of the piecewise function f(x) to find the following
-
(Multiple Choice)
4.8/5  (44)
(44)
Solve.
-Use the formula , , where is the number of items at time , is the initial amount, and is a growth constant equal to the percent of growth (expressed in decimal form) per unit of time. There are currently 56 million cars in a certain country, increasing by annually. How many years will it take for this country to have 78 million cars? Round to the nearest year.
(Multiple Choice)
4.8/5  (24)
(24)
Graph f(x). State the domain, range, and horizontal asymptote of the function
-
(Multiple Choice)
4.9/5  (25)
(25)
Rewrite as a single logarithm using the quotient rule for logarithms. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (34)
(34)
Graph f(x). State the domain, range, and horizontal asymptote of the function
-
(Multiple Choice)
4.9/5  (32)
(32)
Determine whether the functions and are inverse functions.
-
(Multiple Choice)
4.9/5  (35)
(35)
Given and , find the indicated composition and evaluate.
-
Find .
(Multiple Choice)
4.8/5  (38)
(38)
Expand. A ssume that all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (35)
(35)
Evaluate. Round to the nearest thousandth, if necessary.
-
(Multiple Choice)
4.9/5  (27)
(27)
Rewrite using the pow er and product rules. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (29)
(29)
Showing 241 - 260 of 404
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)