Exam 9: Logarithmic and Exponential Functions
Exam 1: Review of Real Numbers152 Questions
Exam 2: Linear and Absolute Value Equations and Inequalities334 Questions
Exam 3: Graphing Linear Equations353 Questions
Exam 4: Systems of Equations204 Questions
Exam 5: Exponents, Polynomials, and Factoring Polynomials453 Questions
Exam 6: Rational Expressions and Equations249 Questions
Exam 7: Radical Expressions and Equations361 Questions
Exam 8: Quadratic Equations270 Questions
Exam 9: Logarithmic and Exponential Functions404 Questions
Exam 10: Conic Sections122 Questions
Exam 11: Sequences, Series, and the Binomial Theorem154 Questions
Select questions type
Expand. A ssume that all variables represent positive real numbers.
-
(Multiple Choice)
4.7/5  (38)
(38)
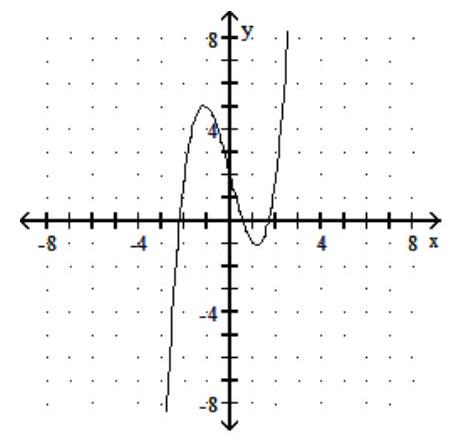
Use the horizontal-line test to determine whether the function is one to one.
-
(True/False)
4.7/5  (35)
(35)
Given and , find the indicated composition and state its domain.
-
Find .
(Multiple Choice)
4.7/5  (29)
(29)
For the given functions and , find or as indicated.
-
Find .
(Multiple Choice)
4.9/5  (47)
(47)
Find the specified domain
-For and , what is the domain of ?
(Multiple Choice)
4.9/5  (27)
(27)
Graph the given function f(x). Label the vertical asymptote. State the domain and range of the function.
-Let .. Solve .
(Multiple Choice)
4.8/5  (36)
(36)
Evaluate the given function. Round to the nearest thousandth.
-
(Multiple Choice)
4.9/5  (33)
(33)
Determine the equation of the vertical asymptote for the graph of this function, and state the domain and range of this function.
-
(Multiple Choice)
4.9/5  (27)
(27)
Rewrite in terms of two or more logarithms using the quotient and product rules for logarithms. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (37)
(37)
Rew rite as a single logarithm. A ssume all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (29)
(29)
Graph f(x). State the domain, range, and horizontal asymptote of the function
-
(Multiple Choice)
4.9/5  (33)
(33)
The decay of of an isotope is given by , where is time in years since the initial amount of was present. Find the amount left (to the nearest ) after 71 years.
(Multiple Choice)
4.9/5  (34)
(34)
Showing 381 - 400 of 404
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)