Exam 9: Logarithmic and Exponential Functions
Exam 1: Review of Real Numbers152 Questions
Exam 2: Linear and Absolute Value Equations and Inequalities334 Questions
Exam 3: Graphing Linear Equations353 Questions
Exam 4: Systems of Equations204 Questions
Exam 5: Exponents, Polynomials, and Factoring Polynomials453 Questions
Exam 6: Rational Expressions and Equations249 Questions
Exam 7: Radical Expressions and Equations361 Questions
Exam 8: Quadratic Equations270 Questions
Exam 9: Logarithmic and Exponential Functions404 Questions
Exam 10: Conic Sections122 Questions
Exam 11: Sequences, Series, and the Binomial Theorem154 Questions
Select questions type
Graph. State the domain, range, and vertical asymptote of the function
-
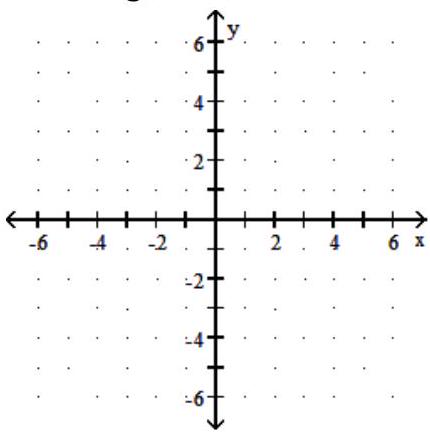
(Multiple Choice)
4.9/5  (34)
(34)
Expand. A ssume that all variables represent positive real numbers.
-
(Multiple Choice)
4.8/5  (33)
(33)
Use the horizontal-line test to determine whether the function is one to one.
-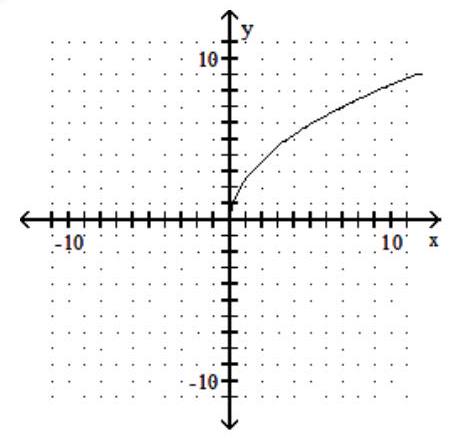
(True/False)
5.0/5  (38)
(38)
Graph the given function f(x). Label the vertical asymptote. State the domain and range of the function.
-
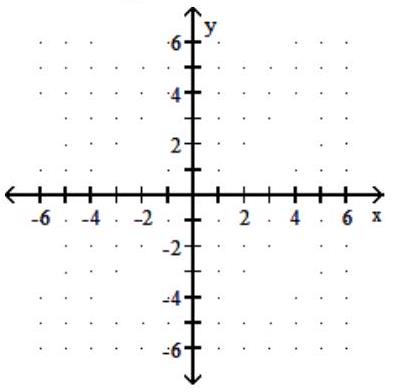
(Multiple Choice)
4.7/5  (34)
(34)
Determine the equation of the horizontal asymptote for the graph of this function, and state the domain and range of thisfunction.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use the horizontal-line test to determine whether the function is one to one.
-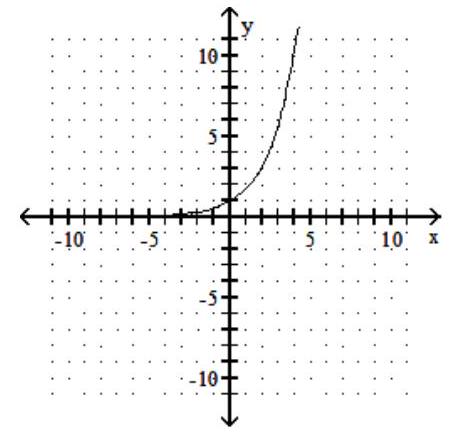
(True/False)
5.0/5  (36)
(36)
Find the missing number. Round to the nearest hundredth if necessary.
-
(Multiple Choice)
4.9/5  (33)
(33)
The area betw een the graph of and the -axis on an interval is equal to . Sketch the graph of , and shade the area between the graph and the -axis. Find the shaded area, rounded to the nearest hundredth.
-
![The area betw een the graph of f(x)=e^{x} and the x -axis on an interval [a, b] is equal to e^{b}-e^{a} . Sketch the graph of f(x)=e^{x} , and shade the area between the graph and the x -axis. Find the shaded area, rounded to the nearest hundredth. - [-2,1]](https://storage.examlex.com/TB10229/11eebb86_1e0c_c924_937f_55dbe80c2b94_TB10229_00.jpg)
(Multiple Choice)
4.8/5  (42)
(42)
Use the formula to find the average rate of change of the function f(x) on the interval [a, b].
-
(Multiple Choice)
4.8/5  (39)
(39)
Another way to approximate the value of is through the sum . The notation represents factorial, which is the product of all the integers from 1 through . The more terms added to the sum, the closer the sum gets to e. In calculus, we say that the limit of this sum is e. Find the sum of the first terms, rounded to the nearest hundred-thousandth, and determine how close the result is to e rounded to the nearest hundred-thousandth (2.71828).
- terms
(Multiple Choice)
5.0/5  (41)
(41)
Solve the problem.
-A college loan of is made at interest, compounded annually. After tyears, the amount due, , is given by the function
After what amount of time will the amount reach ? Round your answer to the nearest tenth.
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-Approximately one fourth of all glass bottles distributed will be recycled each year. A beverage company distributes 310,000 bottles. The number still in use after years is given by the function
After how many years will 30,000 bottles still be in use? Round your answer to the nearest tenth.
(Multiple Choice)
4.8/5  (45)
(45)
Solve.
-The function models the amount in pounds of a particular radioactive material stored in a concrete vault, where is the number of years since the material was put into the vault. If 900 pounds of the material are initially put into the vault, how many pounds will be left after 80 years?
(Multiple Choice)
4.8/5  (39)
(39)
Showing 341 - 360 of 404
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)