Exam 10: Compositions, Inverses, and Combinations of Functions

Let $f(x)=\frac{4}{2+x}$ and let $g(x)=f(f(x))$ . What is $g^{-1}(x)$ ?

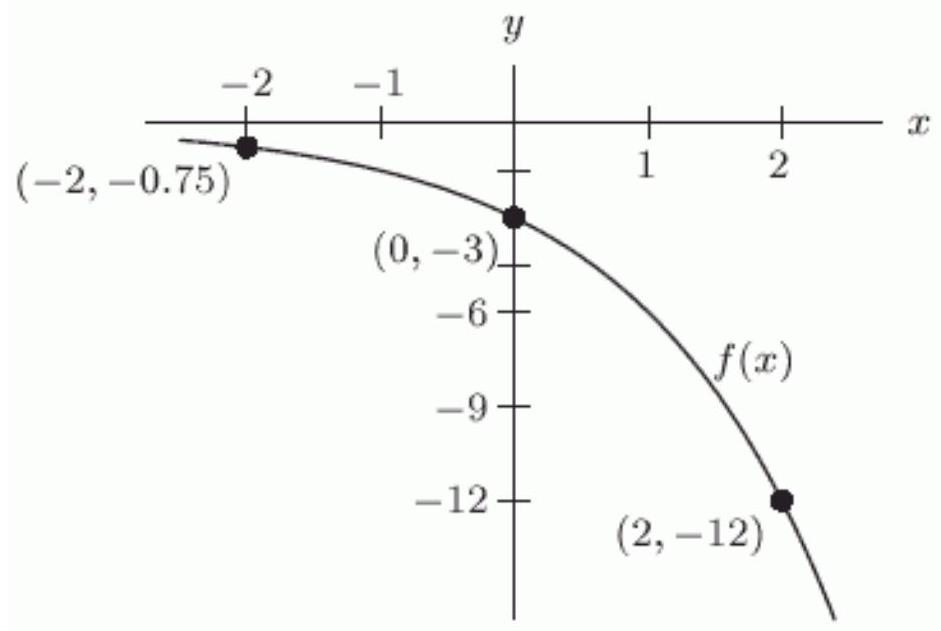
Let $f$ be defined by the following graph. Describe the graph of $y=f(-x)-2$ .

The functions $m(x)$ and $n(x)$ are defined by the graph below. The dashed graph is $m(x)$ and the solid graph is 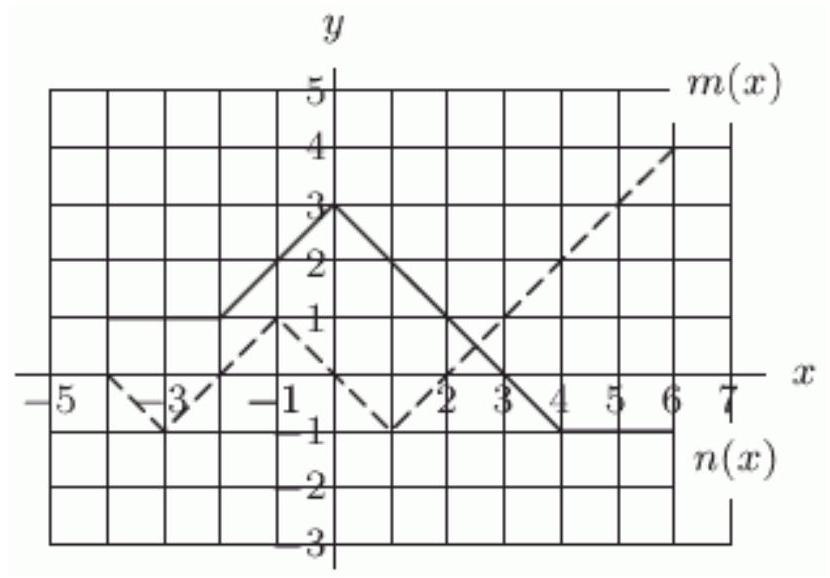$n(x)$ . Evaluate $m(-3) \cdot n(-3)$ .

For $f(x)=\frac{6}{x}$ , does $\frac{f(x+h)-f(x)}{h}=\frac{6}{x^{2}+h x}$ ?

Find the function $p(x)=f(x)+g(x)$ when $f(x)=4 x+1$ and $g(x)=2 x+6$ .

The following table gives values for the functions $f, g$ , and $h$ , three functions defined only for the values $x=0,1, \ldots, 5$ . Based on the table, what is $2 f(3)+g(h(3))$ ?

If $p(q(x))=\frac{4}{1+x}$ and $q(x)=5+x$ , what is $p(x)$ ?

If $y=\frac{3 x^{2}+1}{6 x^{2}}=u(v(x))$ , which of the following could be true? Mark all that apply.

Given $f^{-1}(x)=400(1.02)^{x}$ , what is $f(x)$ ?

Let $f(x)=2^{x}$ and $g(x)=f(f(x))$ . Evaluate $g^{-1}(11)$ to 2 decimal places.

Use a graph to determine whether or not $y=6 x^{5}+3$ is invertible.

Let $f(x)=\cos (7 x)$ and $g(x)=\sqrt{1-x^{2}}$ . What is $g(f(x))$ ?

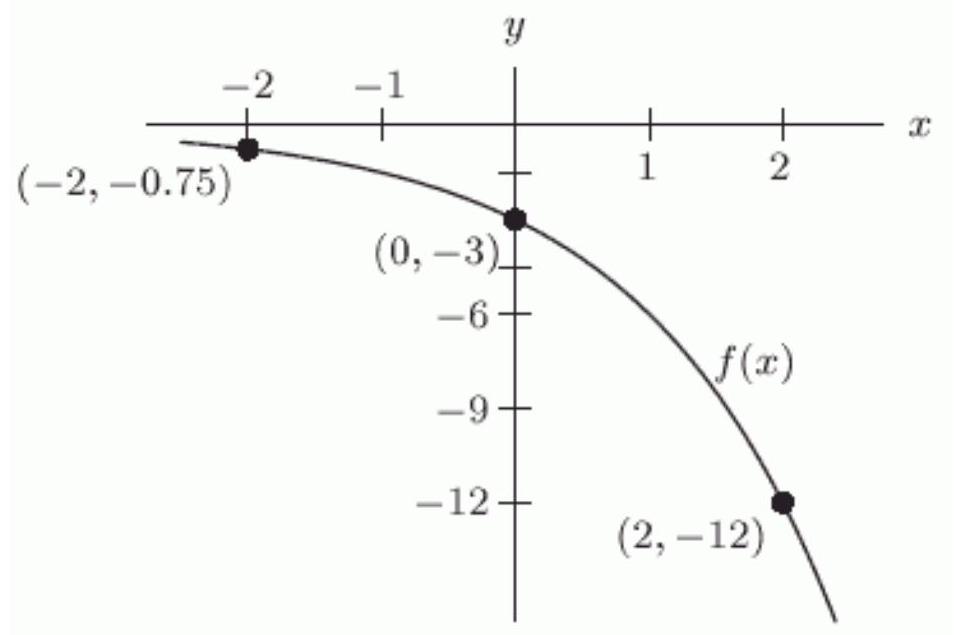
Let $f$ be defined by the following graph. Describe the graph of $y=(-2) f(x)$ .

Let $f(x)=x^{2}+1$ and $h(x)=\sqrt{x-5}$ . Does $f(h(x))=x-24$ ?

Find a simplified formula for $h$ given $F(x)=4 x^{3} f(x)=12 x^{2}$ $G(x)=e^{5 x} g(x)=5 e^{5 x}$ $h(x)=\frac{f(x) G(x)-F(x) g(x)}{(G(x))^{2}}$

What is the inverse of $f(x)=\frac{4 x+1}{4 x-1}$ ?

A child building a tower with blocks places 18 blocks in the first row, 17 blocks in the second row, 16 blocks in the third row, and so forth. How many blocks are in the $10^{\text {th }}$ row?

Given $f^{-1}(x)=800(1.05)^{x}$ , solve $f^{-1}(x)=1000$ . Round to 3 decimal places.

Let $f(x)=\frac{4}{x+1}$ . Find and simplify $f\left(\frac{1}{x}\right)-\frac{1}{f(x)}$ .

Let $f(t)$ be the number of men and let $g(t)$ be the number of women residing in a certain town in year $t$ . Let $h(t)$ be the average income, in dollars, of residents of that town in year $t$ . If $f(t)=250+5 t, g(t)=275+7 t$ , and $h(t)=32,000+200 t$ , find the total amount of money earned by all adult residents of the town in year 3 .