Exam 10: Compositions, Inverses, and Combinations of Functions
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
The function is shown in the first figure.
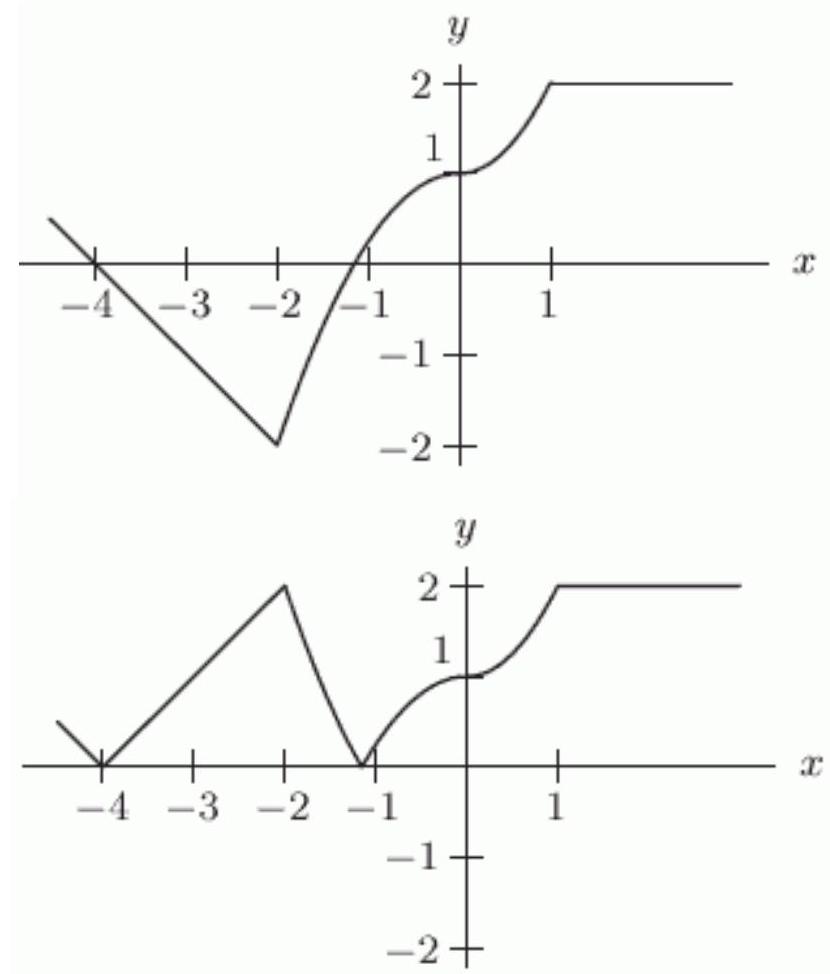 Which transformation of is shown in the second figure?
Which transformation of is shown in the second figure?
(Multiple Choice)
4.8/5  (38)
(38)
Given the graph of below, which of the following is a solution to the equation ?
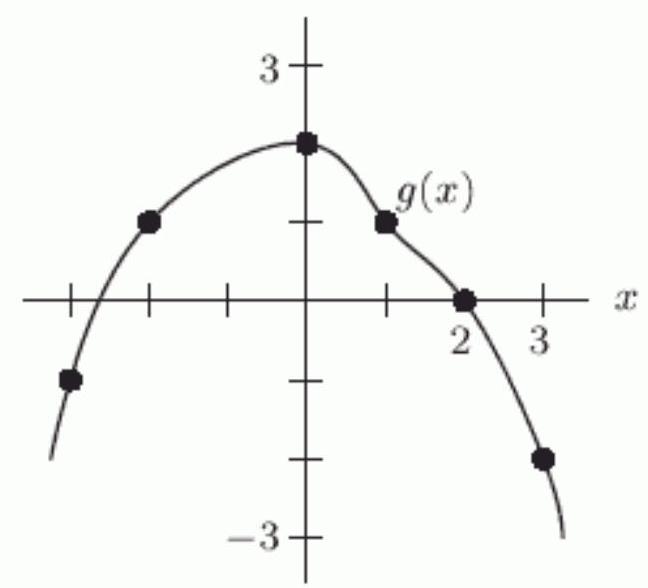
(Multiple Choice)
4.9/5  (35)
(35)
Let and . Using the table below gives -----------and -----------------
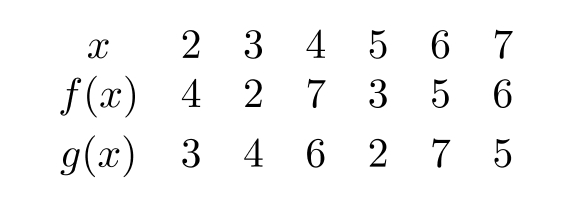
(Short Answer)
4.9/5  (34)
(34)
Showing 61 - 69 of 69
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)