Exam 12: Vectors and Matrices
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
In the figure below, each square is 6 units along each side. In component form, ------------- ---------- .
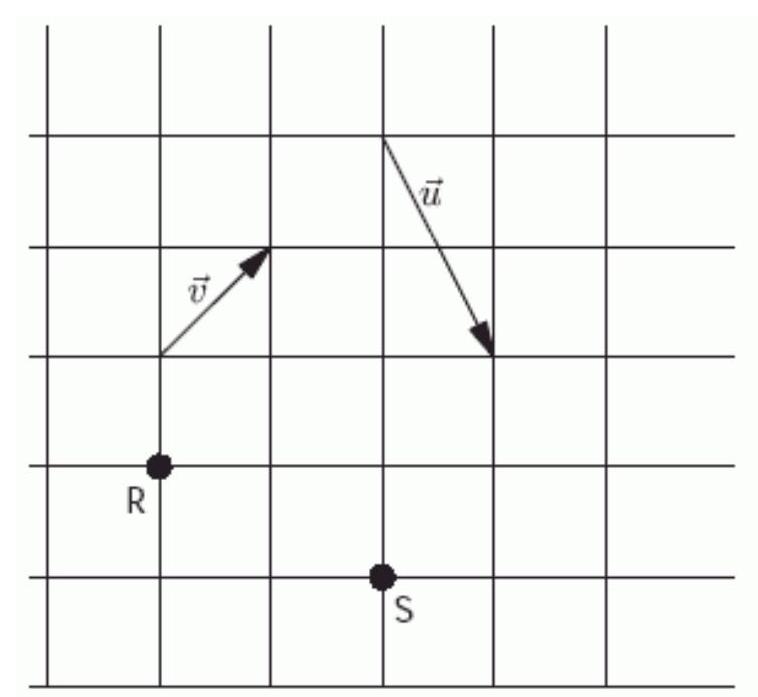
(Short Answer)
4.7/5  (41)
(41)
How many ft-lbs of work are required to lift a 371 pound refrigerator 3 inches straight up? Round to 2 decimal places.
(Short Answer)
4.8/5  (39)
(39)
A car travels 19 miles south and then 23 miles east. Which of the following is true?
(Multiple Choice)
4.7/5  (44)
(44)
Let the student vector be the number of ninth, tenth, eleventh, and twelfth graders in a high school. If the number of students in each grade increases by 5 , what is the new student vector ?
(Short Answer)
4.9/5  (40)
(40)
Let the student vector be the number of ninth, tenth, eleventh, and twelfth graders in a high school. If the number of students in each grade doubles, what is the new student vector ?
(Short Answer)
4.8/5  (30)
(30)
In the figure below, each square is 9 units along each side. In component form, 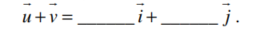
(Short Answer)
4.8/5  (39)
(39)
Does point in the same direction as , the opposite direction, or neither?
(Short Answer)
4.9/5  (32)
(32)
Jack and Jill begin walking away from a water well. Jill walks 2 meters north, and then 12 meters east. When Jill stops, Jack is twice as far from the well as she is. How far is Jack from the well? Round numbers to 3 decimal places if necessary.
(Short Answer)
4.8/5  (31)
(31)
Jack and Jill begin walking away from a water well. Jill walks 4 meters west, and then 2 meters north. When Jill stops, Jack is three times as far from the well as she is, but in the opposite direction. If is the vector pointing from Jack to the well, find the length and direction of . Round numbers to 3 decimal places if necessary.
(Short Answer)
4.8/5  (46)
(46)
The rectangle with vertices , and is rotated through an angle of about the origin. What are the coordinates of the new rectangle? Round numbers to 3 decimal places if necessary.
(Short Answer)
4.8/5  (40)
(40)
A cannon is fired at a angle with the ground at a speed of . Resolve the velocity vector into horizontal and vertical components.
(Short Answer)
4.8/5  (39)
(39)
Showing 61 - 80 of 104
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)