Exam 12: Vectors and Matrices
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
The unit vector from the point toward the point has its head at the point ( -------------,------------). Round to 2 decimal places.
(Short Answer)
4.8/5  (38)
(38)
A man leaves his car and walks 2 miles northeast, 4 miles east, and then 8 miles southwest. How far is the person from his car? In what direction must he walk to head directly to his car? Round numbers to 3 decimal places if necessary.
(Short Answer)
4.9/5  (29)
(29)
The inverse of a matrix , denoted by , is such that if , then . For a matrix , the inverse is given by , where is undefined if Let . Does
(True/False)
4.9/5  (40)
(40)
A snow cone stand sells three sizes of snow cones: small, medium, and large. Let give the number of each type of cone sold in one day. Let give the price charged for each size of snow cone, give the cost of making each size of snow cone, and give the maximum number of each size that can be sold (because of the number of each size cup on hand.) Let . Which of the following gives the total profit earned in one day?
(Multiple Choice)
4.8/5  (40)
(40)
Let be the population vector of a city giving , the number of people who own their home and , the number of people who rent. Suppose that each year, 3\% of the people who own their home move to a rental and of the people who rent purchase a home and become owners. Let be such that . What is ?
(Short Answer)
4.7/5  (42)
(42)
In the figure below, each square is 7 units along each side. The vector perpendicular to the displacement vector is ----------- .
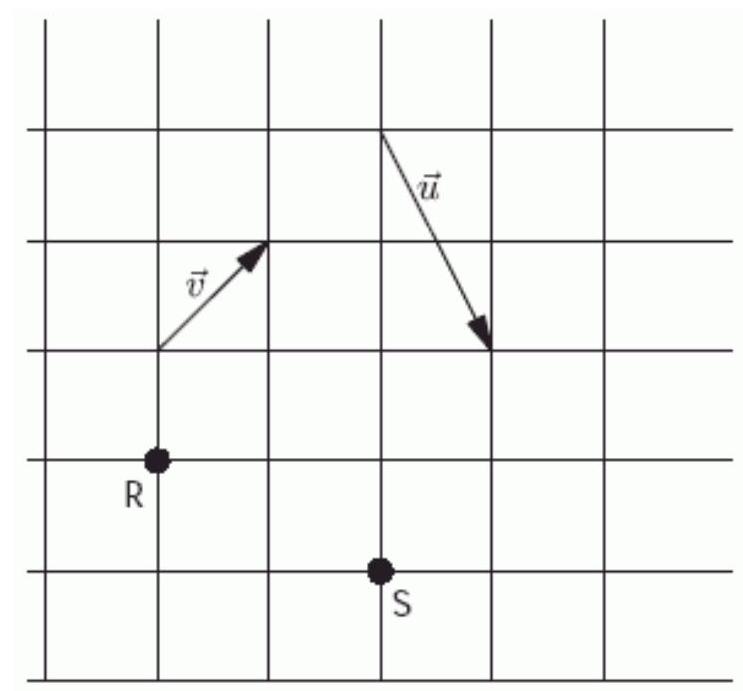
(Short Answer)
5.0/5  (39)
(39)
How many ft-lbs of work are done pushing a stroller with a toddler in it up a 45 yard hill if the slope of the hill is ? Round to 1 decimal place.
(Short Answer)
4.8/5  (35)
(35)
A country has two main political parties. The vector gives the number of people who are members of the first party, the second party, and neither party, respectively. Suppose . Let be the population vector (in tens of thousands) in the year 2005. What is ?
(Short Answer)
4.8/5  (27)
(27)
A cyclist goes at 6 mph due north and feels the wind coming against him at a relative velocity of 3 mph due west. The actual velocity of the wind is ----------mph at an angle of ---------------°west of north. Round both answers to 1 decimal place.
(Short Answer)
5.0/5  (41)
(41)
An airplane flies at an airspeed of in a cross-wind that is blowing from the southwest at a speed of . What direction should the plane fly to end up going due south?
(Short Answer)
4.8/5  (33)
(33)
Let be a vector of length 3 pointing north of east. Find the length and direction of .
(Short Answer)
4.9/5  (28)
(28)
The angle between the vectors and is---------. Round to the nearest whole number.
(Short Answer)
4.8/5  (33)
(33)
Showing 21 - 40 of 104
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)