Exam 12: Vectors and Matrices
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
A country has two main political parties. The vector gives the number of people who are members of the first party, the second party, and neither party, respectively. Suppose . Let be the population vector (in tens of thousands) in the year 2005. What is ?
(Short Answer)
4.8/5  (32)
(32)
Is the distance between a satellite and the earth a vector or a scalar?
(Short Answer)
4.9/5  (31)
(31)
A country has two main political parties. The vector gives the number of people who are members of the first party, the second party, and neither party, respectively. Suppose . Which party's members are the most loyal?
(Multiple Choice)
4.7/5  (33)
(33)
The vector starting at the point and ending at the point can be resolved into the components ----------------- --------------
(Short Answer)
4.8/5  (38)
(38)
A retailer's total monthly sales of three different models of television is given by the vector . If the sales for each model go up by 7 the next month, what is , the next month's total sales?
(Short Answer)
4.7/5  (36)
(36)
A horse runs at a constant speed of . He starts at a fence and his path makes an angle of with the fence. After 9 seconds, how far is he from the fence? Round numbers to 3 decimal places if necessary.
(Short Answer)
4.8/5  (33)
(33)
A particle in equilibrium is acted upon by three forces, two of which have components and . The components of the third must be ------ .
(Short Answer)
4.8/5  (43)
(43)
In the figure below, the angle between the -axis and the vector is------------° Round to the nearest whole number.
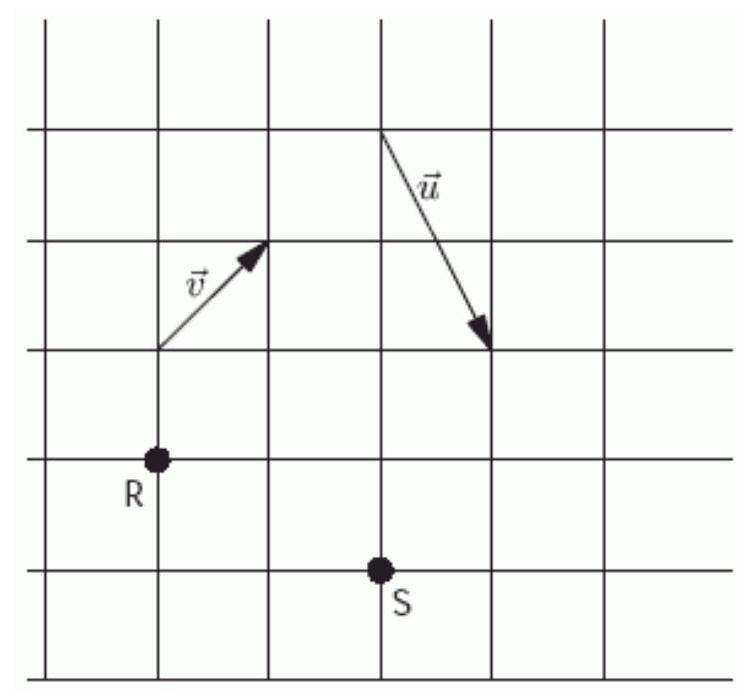
(Short Answer)
4.9/5  (32)
(32)
A particle is acted on by two forces, one of them to the west and of magnitude 0.5 dynes (a dyne is a unit of force), and the other in the direction north of east and of magnitude 1 dyne. A third force acting upon the particle that would keep it at equilibrium has a magnitude of ------- dynes and points ------------(north \ south \ east \ west). Round the first answer to 2 decimal places.
(Short Answer)
4.8/5  (42)
(42)
Let and . Find a vector of length 9 pointing in the opposite direction of .
(Short Answer)
4.9/5  (29)
(29)
A model pyramid is built using four equilateral triangles connected to a square base. If the length of one side of the base is 11 inches, how many inches high is the pyramid? Round to 2 decimal places.
(Short Answer)
4.9/5  (49)
(49)
Let be a vector of length 3 pointing north of east. Find the length and direction of .
(Short Answer)
4.7/5  (37)
(37)
An airplane is flying at an airspeed of 600 km/hr in a crosswind blowing from the southeast at a speed of 50 km/hr. To end up going due west, the plane should head ------------° south of west and will have a speed of ----------- km/hr relative to the ground. Round each answer to 2 decimal places.
(Short Answer)
4.9/5  (34)
(34)
Showing 81 - 100 of 104
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)