Exam 13: Integral Calculus
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Estimate the value of the quantity
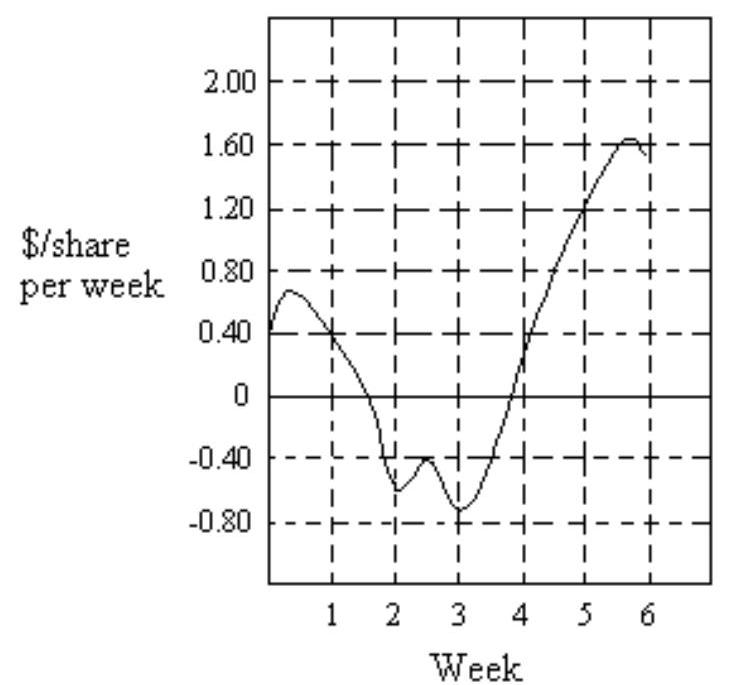
-The graph below shows the rate of change of the price of a stock (in dollars per share per week) over a period of 6 weeks. Estimate the total change in dollars per share of the stock during this period. Use rectangles with widths of 1 week and let the function value at the midpoint of the rectangle give the height of the rectangle.
(Multiple Choice)
4.9/5  (32)
(32)
Find the given indefinite integral. State whether integration by substitution or integration by parts was used.
-
(Multiple Choice)
4.8/5  (38)
(38)
Use the definite integral to find the area between the -axis and the graph of over the indicated interval.
-
(Multiple Choice)
4.8/5  (39)
(39)
A student has a supply equation and selling price. What kind of surplus can the student calculate with this information?
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-Suppose that an object's acceleration function is given by . The object's initial velocity, , is 3 , and the object's initial position, , is 12 . Find .
(Multiple Choice)
4.7/5  (40)
(40)
Solve the problem.
-Suppose the supply function of a certain item is given by and the demand function is . Find the consumer's surplus.
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-For a certain drug, the rate of reaction in appropriate units is given by , where is measured in hours after the drug is administered. Find the total reaction to the drug from to .
(Multiple Choice)
4.8/5  (43)
(43)
Find the particular solution of the differential equation.
- when
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-Find the consumer's surplus if the demand for an item is given by , assuming supply and demand are in equilibrium at .
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-The velocity (in ) of an object moving with acceleration a (in ) is given by , where is the time (in seconds). Find a formula for , if .
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-The slope to the tangent line of a curve is given by . If the point is on the curve, find an equation of the curve.
(Multiple Choice)
4.8/5  (41)
(41)
Showing 101 - 120 of 227
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)