Exam 3: Functions and Graphs
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Determine whether the following rule defines as a function of .
-
Free
(True/False)
4.9/5  (29)
(29)
Correct Answer:
True
Solve the problem.
-The manager of a CD store has found that if the price of a CD is , then will be sold. Find an expression for the total revenue from the sale of CDs
(hint: revenue demand price). Use your expression to determine the maximum revenue.
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
D
Solve the problem.
-Regrind, Inc. regrinds used typewriter platens. The cost per platen is . The fixed cost to run the grinding machine is per day. If the company sells the reground platens for , how many must be reground daily to reach the break-even point?
(Multiple Choice)
4.7/5  (33)
(33)
Find the appropriate linear cost or revenue function.
-Find the revenue function given the following information. Fixed cost: ; marginal cost per item: ; item sells for
(Multiple Choice)
4.8/5  (17)
(17)
Solve the problem.
-Suppose the supply and demand for a certain videotape are given by:
Where is price and is quantity.
Find the equilibrium demand.
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-A ball is thrown vertically upward at an initial speed of . Its height (in feet) after seconds is given by
After how many seconds does the ball reach its maximum height?
(Multiple Choice)
4.7/5  (42)
(42)
Solve the problem.
-The demand for a certain type of modem is given by
Where is the price when units are demanded. Determine the price that will produce the maximum revenue. (Hint: First find the revenue , that would be obtained at a demand of ).
(Multiple Choice)
4.9/5  (42)
(42)
Solve the problem.
-Suppose a car rental company charges for the first day and for each additional or partial day. Let represent the cost of renting a car for days. Find the value of .
(Multiple Choice)
4.9/5  (29)
(29)
Find a quadratic function that models the data.
-The table shows the population of a city in selected years. Data are in thousands rounded to the nearest hundred.
 Let correspond to 1970 and let be the population of the city (in thousands) in year . Using the point as the vertex and and the data from 1995, determine a quadratic function that models the data.
Let correspond to 1970 and let be the population of the city (in thousands) in year . Using the point as the vertex and and the data from 1995, determine a quadratic function that models the data.
(Multiple Choice)
4.9/5  (32)
(32)
Find the rule of a quadratic function whose graph has the given vertex and passes through the given point.
-vertex ; point
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-The graph of a function is given below. Tell whether the graph could possibly be the graph of a polynomial function. If it could be the graph of a polynomial function, tell which of the following are possible degrees for the polynomial function: 3, 4, 5, 6 .
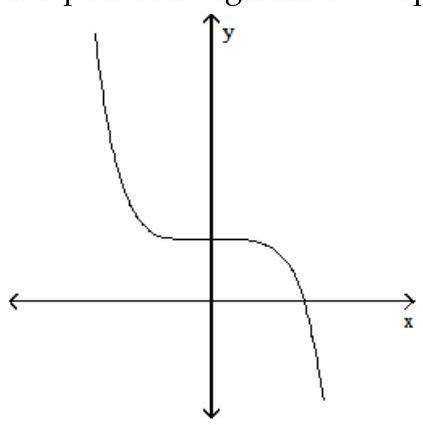
(Multiple Choice)
4.7/5  (30)
(30)
Solve the problem.
-The graph of a function is given below. Tell whether the graph could possibly be the graph of a polynomial function. If it could be the graph of a polynomial function, tell which of the following are possible degrees for the polynomial function: .
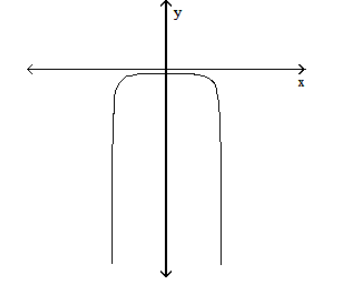
(Multiple Choice)
4.9/5  (33)
(33)
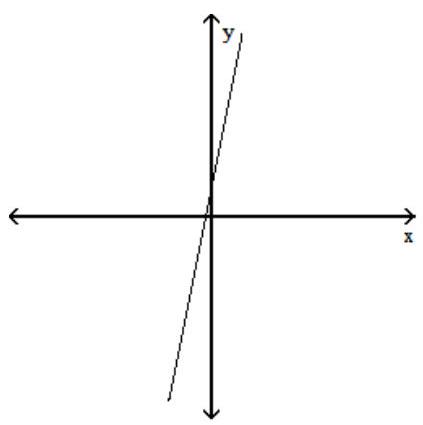
Use the vertical line test to determine if the graph is a graph of a function.
-
(True/False)
4.7/5  (31)
(31)
Give the equation of the horizontal asymptote of the rational function.
-
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-The graph of a function is given below. Tell whether the graph could possibly be the graph of a polynomial function. If it could be the graph of a polynomial function, tell which of the following are possible degrees for the polynomial function: .
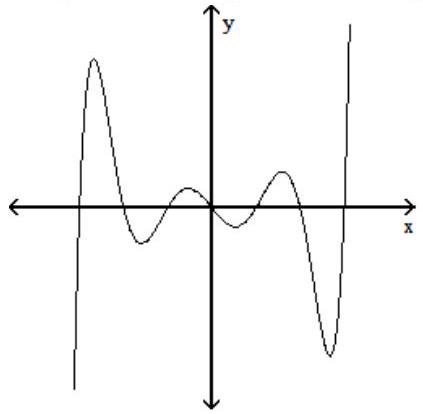
(Multiple Choice)
4.8/5  (41)
(41)
Showing 1 - 20 of 323
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)