Exam 9: Counting, Probability Distributions, and Further Topics in Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Find the equilibrium vector for the transition matrix.
-
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
A
Find the equilibrium vector for the transition matrix.
-
Free
(Multiple Choice)
5.0/5  (32)
(32)
Correct Answer:
D
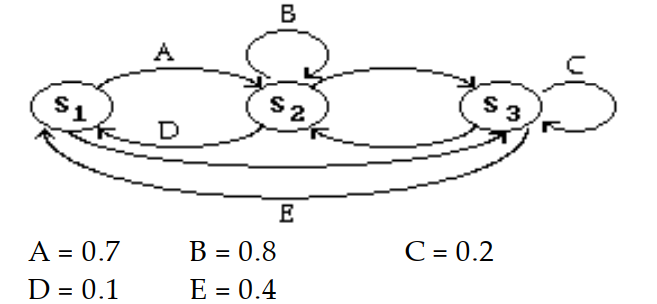
Construct the transition matrix for the transition diagram.
-
(Multiple Choice)
4.7/5  (37)
(37)
Use the payoff matrix to determine the best strategy.
-A computer manufacturer must decide whether or not to market a new product. The new product may or may not be better than the old product. If they market the new product and it is better than the old product, their sales should increase. If they market the new product and it is not better, they will lose money to competitors. If they do not market the new product, they will lose to competitors if it is actually better and will lose just the research costs if it is not better. The manufacturer estimates that the payoff matrix is as follows:
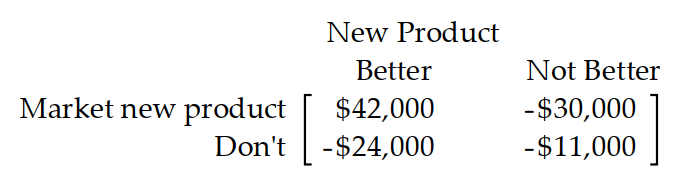 The manufacturer believes that the probability that the new product is better is 0.1 . What is the best strategy?
The manufacturer believes that the probability that the new product is better is 0.1 . What is the best strategy?
(Multiple Choice)
4.9/5  (35)
(35)
Prepare a probability distribution for the experiment. Let represent the random variable, and let represent theprobability.
-Four cards are drawn from a deck. The number of red tens is counted.
(Multiple Choice)
4.8/5  (22)
(22)
Solve the problem.
-How many distinguishable permutations of letters are possible using the letters in the word COLORADO?
(Multiple Choice)
4.7/5  (34)
(34)
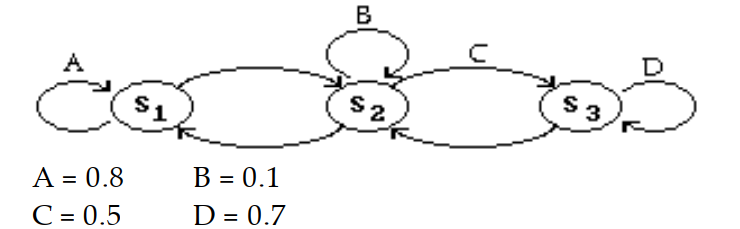
Construct the transition matrix for the transition diagram.
-
(Multiple Choice)
4.7/5  (25)
(25)
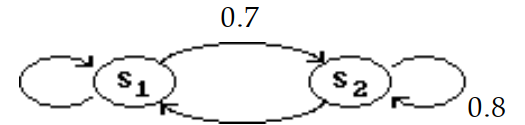
Construct the transition matrix for the transition diagram.
-
(Multiple Choice)
4.8/5  (32)
(32)
For the transition matrix, find the probability that state 2 changes to state 4 after 5 repetitions of the experiment.
-
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-How many distinguishable permutations of letters are possible using the letters in the word CRITICS?
(Multiple Choice)
4.8/5  (23)
(23)
Solve the problem.
-Amy has 3 blue, 2 red, and 5 green books to arrange on a shelf. In how many distinguishable ways can the books be arranged if books of the same color are identical?
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Five cards are drawn at random from an ordinary deck of 52 cards. In how many ways is it possible to draw two red aces and two black jacks?
(Multiple Choice)
4.7/5  (38)
(38)
Find the probability of the event.
-On a hospital floor, 16 patients have a disease with a mortality rate of .1. Two of them die.
(Multiple Choice)
4.8/5  (32)
(32)
Showing 1 - 20 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)