Exam 7: S Advanced Waiting Line Theory and Simulation Modeling
Gerard is choosing between two methods of organizing his bakery.Method one will require a counter person to wait on each customer individually before they proceed to the cashier to pay for their purchases.In this system,customers will arrive at the rate of 8 per hour and can be served by the counter person at the rate of 15 per hour.The cashier will be capable of serving customers at the rate of 20 per hour.For simplification purposes,assume that the arrival rate at the cashier phase is identical to the arrival rate at the first phase and that these waiting lines can be analyzed independently and combined.
Method two will have the two employees wait on customers as they select their pastries and also collect their money once their selections have been made.Customers still arrive at the rate of 8 per hour but now the total service time (pastry selection and payment collection)takes 5 minutes per customer.Calculate the average number of customers in the bakery and the average time spent in the bakery for both systems and make your recommendations to Gerard.
Method one is a two-phase,single server system with an arrival rate into both phases of 8 customers per hour and a service rate at the first phase of 15 customers per hour and the second phase of 20 customers per hour.
The average number of customers in the bakery will be the sum of the customers at the counter and at the cashier.
At the counter step:
CSCounter= CWCounter + 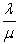
= 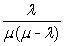
+ 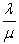
CSCounter = 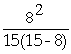
+ 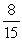
= 1.1429 customers
At the cashier step:
CSCashier = CWCashier + 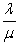
= 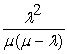
+ 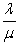
CSCashier = 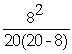
+ 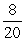
= 0. 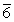
customers
So the total number in the bakery is 1.1429+0.666 = 1.81 customers.
The average time spent in the bakery will be the sum of the times spent waiting and being served in both phases.
At the counter step:
TSCounter = TWCounter + 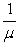
= 
+ 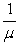
TSCounter = 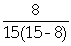
+ 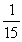
= 0.1429 hours
At the cashier step:
TSCashier = TWCashier + 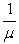
= 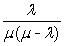
+ 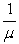
TSCashier = 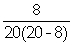
+ 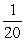
= 0.0833 hours
So the total time in the bakery is 0.1429+0.0833 = 0.2262 hours
Method two is a multiple server system with an arrival rate of 8 customers per hour and a service rate of 12 customers per hour.This analysis requires calculating the probability of zero customers in the system.
P0= 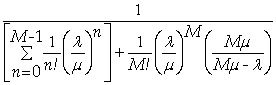
P0 = 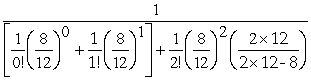
P0 = 0.5
The average number of customers in the system for method two is:
CS = 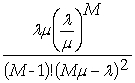
P0 + 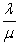
CS = 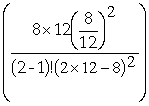
0.5 + 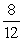
CS = 0.75 customers
The average time spent in the bakery for method 2 is:
TS = 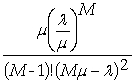
P0 + 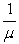
TS = 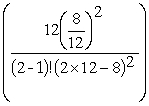
0.5 + 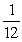
TS = 0.0938 hours
To summarize:
 Method 1
Method 1
One advantage of simulation modeling is:
A
Customers enter the stadium and purchase refreshments before they are shown to their seats by experienced ushers.The concession stand lines are considered elements in the simulation model.
True
A single channel single server system requires that the ________ rate be larger than the ________ rate.
The Greek letter lambda (λ)is used to represent the service rate of a waiting line system.
Customers enter the stadium and purchase refreshments before they are shown to their seats by experienced ushers.The customers are considered objects in the simulation model.
Barber College is the best deal in town! For only $5,you can get a shampoo and cut by any one of four untrained stylists completed in 7.5 minutes on average.Perhaps this is why customers show up on average two minutes apart (both interarrival times and service times are exponentially distributed).
-Develop a full description of the system performance.How much does performance improve if another barber is added to the customer service staff?
Simulation permits the modeler to discover what might happen should certain events occur,for example,extreme levels of customer demand,equipment malfunction,etc.This type of analysis is known as ________ analysis.
Management is concerned about the waiting time for customers and decides to train one more student.If the arrival and service rates remain the same as in the original scenario,what happens to the number of customers in the system?
Customers pass by any one of forty ticket takers on their way in the arena for a WWE event.This is a single ________ system.
In most cases,simulation models provide optimal solutions to problems just like most of the equations presented in your textbook.
The department chair is out of town at a conference and you,as the assistant department chair,find yourself besieged by dozens of students needing permission to get into a very popular (but closed)class.Student arrivals are governed by the Poisson distribution with a mean of 10 minutes.Telling the students that they can't get into the closed class takes about 3 minutes,and this average is exponentially distributed.About how many students are waiting outside your office door?
It is more costly to create a more realistic simulation than one that is less realistic.
A customer enters a business and has the opportunity to select any one of three lines to receive service.The service is performed by one customer service representative after which the customer leaves the establishment.Which description of this waiting line system is appropriate?
Which of the following is characteristic of Monte Carlo simulation?
The bank manager of a busy downtown location found herself unable to find good teller help so she invested in an ATM to handle the routine withdrawals that tended to occupy an inordinate amount of the teller's time.Before she installed the ATM she found that customers were arriving on average every 2 minutes (Poisson distributed)and it took a teller 30 seconds (exponentially distributed)to process their request.The ATM is able to maintain a constant 30 second service time.What is the impact on system utilization?
In most waiting line models,customers are assumed to arrive at random intervals,based on a normal distribution.
Just before he retired for the evening,Saba started his simulation program to simulate five years of hospital operations as he slept.His ability to generate five years of data overnight is a textbook example of ________.
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)