Exam 4: Discrete Random Variables and Probability Distributions
Exam 1: Describing Data: Graphical247 Questions
Exam 2: Describing Data: Numerical326 Questions
Exam 3: Probability345 Questions
Exam 4: Discrete Random Variables and Probability Distributions257 Questions
Exam 5: Continuous Random Variables and Probability Distributions239 Questions
Exam 6: Sampling and Sampling Distributions147 Questions
Exam 7: Estimation: Single Population151 Questions
Exam 8: Estimation: Additional Topics109 Questions
Exam 9: Hypothesis Testing: Single Population164 Questions
Exam 10: Hypothesis Testing: Additional Topics103 Questions
Exam 11: Simple Regression217 Questions
Exam 12: Multiple Regression252 Questions
Exam 13: Additional Topics in Regression Analysis168 Questions
Exam 14: Analysis of Categorical Data241 Questions
Exam 15: Analysis of Variance192 Questions
Exam 16: Time-Series Analysis and Forecasting138 Questions
Exam 17: Additional Topics in Sampling110 Questions
Select questions type
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
Consider the following probability distribution function.
 -What is P(X < 6)?
-What is P(X < 6)?
(Essay)
4.7/5  (41)
(41)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
The number of accidents on a particular highway averages 4.4 per year.Assume that the number of accidents follows a Poisson distribution.
-What is the probability that there are more than three accidents next year?
(Multiple Choice)
4.8/5  (31)
(31)
What is the probability that no one is waiting or being served in the express checkout line?
(Essay)
4.8/5  (35)
(35)
In dealing with a pair of jointly distributed discrete random variables,the conditional probability distribution on one random variable,given specified values of another,is the:
(Multiple Choice)
4.8/5  (32)
(32)
The correlation coefficient r is a number that indicates the direction and the strength of the relationship between two random variables.
(True/False)
4.8/5  (37)
(37)
One characteristic of the binomial distribution is that the outcome of one trial does not affect the outcome of any other trial.
(True/False)
4.8/5  (35)
(35)
In basketball,one of the possible penalties after a foul is called a free throw.The fouled player gets one shot at the basket from the foul line.If he misses this shot,he is awarded no points and the penalty is over.If he makes the shot,then he gets one point and gets to take another shot.If he makes the second shot he gets an additional point,and the ball is turned over to the other team.If he misses the second shot,the penalty is over.Suppose that the probability of making a shot is 80%,and the likelihood of making one shot is independent of the outcome of any other shot.What is the probability distribution function for the points from the penalty? On average,how many points would you expect to get from the penalty?
(Essay)
4.7/5  (32)
(32)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
A basketball player makes 80 percent of his free throws during the regular season.Consider his next eight free throws.
-What is the expected number of free throws that he will make?
(Multiple Choice)
4.9/5  (36)
(36)
The number of rainy days per month at Seattle follows a Poisson distribution with a mean value of 4.5 days.What is the probability that it will rain 3 days next month?
(Multiple Choice)
4.7/5  (32)
(32)
Consider the following probability distribution function.Compute the mean and standard deviation of X.

(Essay)
4.8/5  (34)
(34)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
In a shipment of 18 trucks to a local truck dealer,there are four trucks that don't have air conditioning.Assume that you select four trucks at random.
-What is the probability that two or fewer of the four don't have air conditioning?
(Multiple Choice)
4.8/5  (42)
(42)
The binomial probability distribution is always negatively skewed.
(True/False)
4.9/5  (38)
(38)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
The quality of computer disks is measured by sending the disks through a certifier which counts the number of missing pulses.A certain brand of computer disks averages 0.1 missing pulse per disk.Let the random variable X denote the number of missing pulses.
-Find the probability neither of the next two disks inspected will contain any missing pulse.
(Essay)
4.9/5  (37)
(37)
A pair of jointly distributed random variables are said to be independent if and only if their joint probability distribution is the product of their:
(Multiple Choice)
4.8/5  (33)
(33)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
The following table presents the probability distribution function for the number of claims processed per hour at an insurance agency.
 -Which of the following is true?
-Which of the following is true?
(Multiple Choice)
4.9/5  (30)
(30)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
The following table displays the joint probability distribution of two discrete random variables X and Y. 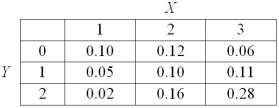 -Compute the expected value for Y.
-Compute the expected value for Y.
(Essay)
4.9/5  (25)
(25)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
Let X be a random variable with the following distribution:
 -Find the expected value of X.
-Find the expected value of X.
(Essay)
4.9/5  (31)
(31)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
The following table presents the probability distribution function for the number of claims processed per hour at an insurance agency.
 -Let a = -μx/σx and b = 1/σx in the linear function Z = a + bX.Which of the following statements is true?
-Let a = -μx/σx and b = 1/σx in the linear function Z = a + bX.Which of the following statements is true?
(Multiple Choice)
4.8/5  (35)
(35)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING:
The number of accidents on a particular highway averages 4.4 per year.Assume that the number of accidents follows a Poisson distribution.
-A recent survey showed that 5 percent of the computer keyboards produced by a particular company are defective.What is the probability that out of eight keyboards selected at random,exactly zero keyboards will be defective?
(Multiple Choice)
4.9/5  (34)
(34)
The probability of various numbers of customers waiting for something to happen,or waiting line or queuing problems in general,are examples of the usefulness of the Poisson distribution.
(True/False)
4.7/5  (33)
(33)
Showing 181 - 200 of 257
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)