Exam 12: Multiple Regression
Exam 1: Describing Data: Graphical247 Questions
Exam 2: Describing Data: Numerical326 Questions
Exam 3: Probability345 Questions
Exam 4: Discrete Random Variables and Probability Distributions257 Questions
Exam 5: Continuous Random Variables and Probability Distributions239 Questions
Exam 6: Sampling and Sampling Distributions147 Questions
Exam 7: Estimation: Single Population151 Questions
Exam 8: Estimation: Additional Topics109 Questions
Exam 9: Hypothesis Testing: Single Population164 Questions
Exam 10: Hypothesis Testing: Additional Topics103 Questions
Exam 11: Simple Regression217 Questions
Exam 12: Multiple Regression252 Questions
Exam 13: Additional Topics in Regression Analysis168 Questions
Exam 14: Analysis of Categorical Data241 Questions
Exam 15: Analysis of Variance192 Questions
Exam 16: Time-Series Analysis and Forecasting138 Questions
Exam 17: Additional Topics in Sampling110 Questions
Select questions type
You have just run a regression in which the value of the multiple coefficient of determination is 0.65.To determine if this indicates that the independent variables explain a significant portion of the variation in the dependent variable,you would perform an F-test.
Free
(True/False)
4.8/5  (40)
(40)
Correct Answer:
True
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
A real estate broker is interested in identifying the factors that determine the price of a house.She wants to run the following regression: Y = β0 + β1X1 + β2X2 + β3X3 + ε where Y = price of the house in $1,000s,X1 = number of bedrooms,X2 = square footage of living space,and X3 = number of miles from the beach.Taking a sample of 30 houses,the broker runs a multiple regression and gets the following results:  = 123.2 + 4.59x1 + 0.125x2 - 6.04x3,
= 123.2 + 4.59x1 + 0.125x2 - 6.04x3, 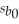 = 103.2,
= 103.2, 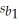 = 2.13,
= 2.13, 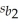 = 0.062,
= 0.062, 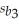 = 4.17,R2 = 0.47,and
= 4.17,R2 = 0.47,and 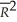 = 0.45 (adjusted).
-What should the null and alternative hypotheses be for β2?
= 0.45 (adjusted).
-What should the null and alternative hypotheses be for β2?
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
A
The standard error of the estimate for a multiple regression model with two explanatory variables X1 and X2:
Free
(Multiple Choice)
4.9/5  (29)
(29)
Correct Answer:
A
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose you are interested in determining the factors that influence the time required to prepare a tax return,and developed the model: Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + ε,where Y is the amount of time (in minutes),X1 is the income of the individual (in thousands of dollars),X2 is the age of the individual,X3 is the number of people living in the household,and X4 is a dummy variable that takes the value 1,if the individual owns his or her own home.After interviewing 40 accountants,you get the following results:  = 17.2 + 3.8x1 - 1.04x2 + 2.15x3 + 15.1x4,
= 17.2 + 3.8x1 - 1.04x2 + 2.15x3 + 15.1x4, 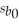 = 5.3,
= 5.3, 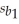 = 0.13,
= 0.13, 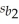 = 0.33,
= 0.33, 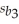 = 1.51,
= 1.51, 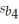 = 4.7,SSR = 164.2,SSE = 200.7,and R2 = 0.45.
-Develop a 95% confidence interval for the population slope β3.
= 4.7,SSR = 164.2,SSE = 200.7,and R2 = 0.45.
-Develop a 95% confidence interval for the population slope β3.
(Short Answer)
4.8/5  (41)
(41)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
A loan officer is interested in examining the determinants of the total dollar value of residential loans made during a month.She used Y = β0 + β1X1 + β2X2 + β3X3 + β4
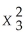 + ε to model the relationship,where Y is the total dollar value of residential loans in a month (in millions of dollars),X1 is the number of loans,X2 is the interest rate,and X3 is the dollar value of expenditures of the bank on advertising (in thousands of dollars).Suppose that by using data from the past 24 months,she obtained
+ ε to model the relationship,where Y is the total dollar value of residential loans in a month (in millions of dollars),X1 is the number of loans,X2 is the interest rate,and X3 is the dollar value of expenditures of the bank on advertising (in thousands of dollars).Suppose that by using data from the past 24 months,she obtained  = 3.8 + 0.23x1 - 1.31x2 + 0.032x3 - 0.0005
= 3.8 + 0.23x1 - 1.31x2 + 0.032x3 - 0.0005 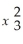 .
-What do these results suggest about the relationship between the total loan amount and advertising?
.
-What do these results suggest about the relationship between the total loan amount and advertising?
(Multiple Choice)
4.7/5  (28)
(28)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
The model y = β0 + β1X1 + β2X2 + ε was fitted to a sample of 25 families in order to explain household milk consumption: where y = Milk consumption,in quarts,per week,x1 = Weekly income,in hundreds of dollars,and x2 = Family size.The least squares estimates of the regression parameters were b0 = -0.03,b1 = 0.05,and b2 = 1.1,with coefficient standard errors 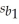 = 0.02;
= 0.02; 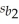 = 0.38.The total sum of squares and the error sum of squares were found to be 165.8 and 66.32 respectively.
-Find 95% confidence interval for β2.
= 0.38.The total sum of squares and the error sum of squares were found to be 165.8 and 66.32 respectively.
-Find 95% confidence interval for β2.
(Essay)
4.9/5  (36)
(36)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
The computer output for the multiple regression model,y = β0 + β1X1 + β2X2 + ε is shown below.However,because of a printer malfunction some of the results are not shown.These are identified by asterisks.
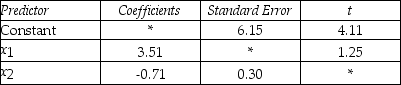 S = * R-Sq = *
ANALYSIS OF VARIANCE
S = * R-Sq = *
ANALYSIS OF VARIANCE
 -Calculate the constant coefficient,b0.
-Calculate the constant coefficient,b0.
(Essay)
4.8/5  (35)
(35)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose you are interested in determining the factors that influence the time required to prepare a tax return,and developed the model: Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + ε,where Y is the amount of time (in minutes),X1 is the income of the individual (in thousands of dollars),X2 is the age of the individual,X3 is the number of people living in the household,and X4 is a dummy variable that takes the value 1,if the individual owns his or her own home.After interviewing 40 accountants,you get the following results:  = 17.2 + 3.8x1 - 1.04x2 + 2.15x3 + 15.1x4,
= 17.2 + 3.8x1 - 1.04x2 + 2.15x3 + 15.1x4, 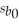 = 5.3,
= 5.3, 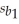 = 0.13,
= 0.13, 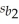 = 0.33,
= 0.33, 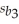 = 1.51,
= 1.51, 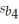 = 4.7,SSR = 164.2,SSE = 200.7,and R2 = 0.45.
-Test H0 : β3 = 0 against H1 : β3 ≠ 0 and interpret your result.
= 4.7,SSR = 164.2,SSE = 200.7,and R2 = 0.45.
-Test H0 : β3 = 0 against H1 : β3 ≠ 0 and interpret your result.
(Essay)
4.8/5  (39)
(39)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below.
THE REGRESSION EQUATION IS:  = 55.8 + 1.79x1 - 0.021x2 - 0.016x3
= 55.8 + 1.79x1 - 0.021x2 - 0.016x3
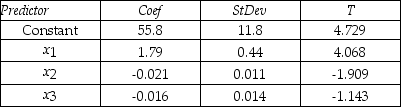 S = 9.47 R-Sq = 22.5%
ANALYSIS OF VARIANCE
S = 9.47 R-Sq = 22.5%
ANALYSIS OF VARIANCE
 -Interpret the coefficient b1.
-Interpret the coefficient b1.
(Essay)
4.8/5  (25)
(25)
What is the approximate p-value associated with the hypothesis test for β2?
(Multiple Choice)
4.8/5  (39)
(39)
In a multiple regression model,the following statistics are given: SSE = 100,R2 = 0.995,K = 5,and n = 15.Determine the multiple coefficient of determination adjusted for degrees of freedom.
(Multiple Choice)
4.8/5  (42)
(42)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
The computer output for the multiple regression model,y = β0 + β1X1 + β2X2 + ε is shown below.However,because of a printer malfunction some of the results are not shown.These are identified by asterisks.
 S = * R-Sq = *
ANALYSIS OF VARIANCE
S = * R-Sq = *
ANALYSIS OF VARIANCE
 -Calculate the multiple coefficient of determination.
-Calculate the multiple coefficient of determination.
(Essay)
4.8/5  (36)
(36)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
The model y = β0 + β1X1 + β2X2 + ε was fitted to a sample of 25 families in order to explain household milk consumption: where y = Milk consumption,in quarts,per week,x1 = Weekly income,in hundreds of dollars,and x2 = Family size.The least squares estimates of the regression parameters were b0 = -0.03,b1 = 0.05,and b2 = 1.1,with coefficient standard errors 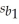 = 0.02;
= 0.02; 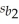 = 0.38.The total sum of squares and the error sum of squares were found to be 165.8 and 66.32 respectively.
-Find 95% confidence interval for β1.
= 0.38.The total sum of squares and the error sum of squares were found to be 165.8 and 66.32 respectively.
-Find 95% confidence interval for β1.
(Essay)
4.7/5  (36)
(36)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
A professor investigated some of the factors that affect an individual student's final grade in his course.He proposed the multiple regression model Y = β0 + β1X1 + β2X2 + β3X3 + ε ,where Y is the final mark (out of 100),X1 is the number of lectures skipped,X2 is the number of late assignments,and X3 is the mid-term test mark (out of 100).The professor recorded the data for 50 randomly selected students.The computer output is shown below.
The regression equation is  = 41.6 - 3.18x1 - 1.17x2 + 0.63x3.
= 41.6 - 3.18x1 - 1.17x2 + 0.63x3.
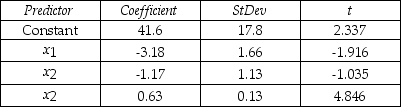 S = 13.74 R-Sq = 30.0%
ANALYSIS OF VARIANCE
S = 13.74 R-Sq = 30.0%
ANALYSIS OF VARIANCE
 -Does the data provide enough evidence to conclude that,at the 5% significance level,the model is useful in predicting the final mark?
-Does the data provide enough evidence to conclude that,at the 5% significance level,the model is useful in predicting the final mark?
(Essay)
4.9/5  (45)
(45)
A multiple regression model that involves 40 observations and 4 independent variables produces SST = 1,000 and SSR = 804.The value of 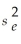 for the model is 5.60.
for the model is 5.60.
(True/False)
4.8/5  (29)
(29)
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
In a study of foreign holdings in Egyptian banks,the following sample regression results were obtained,based on 14 annual observations:  = -3.25 +
= -3.25 + 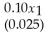 -
- 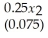 +
+ 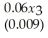 ,and R2 = 0.92,
Where the numbers in parentheses under the coefficient estimates are the estimated coefficient standard errors,and
y = Year-end share of assets in Egyptian bank subsidiaries held by foreigners,as a percentage of total assets
x1 = Annual change,in billions of Egyptian pounds,in foreign direct investment in Egypt
x2 = Bank price-earnings ratio
x3 = Index of the exchange value of the Egyptian pounds
-Find a 95% confidence interval for β2.
,and R2 = 0.92,
Where the numbers in parentheses under the coefficient estimates are the estimated coefficient standard errors,and
y = Year-end share of assets in Egyptian bank subsidiaries held by foreigners,as a percentage of total assets
x1 = Annual change,in billions of Egyptian pounds,in foreign direct investment in Egypt
x2 = Bank price-earnings ratio
x3 = Index of the exchange value of the Egyptian pounds
-Find a 95% confidence interval for β2.
(Essay)
4.9/5  (38)
(38)
Showing 1 - 20 of 252
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)