Exam 8: Estimation: Additional Topics

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: Two dependent random samples from two normally distributed populations gives the following results: n = 10; = 20.5;s_d = 3.2 -Find the lower confidence limit of the 95% confidence interval for the difference between the means of the two populations.

In order to measure the effectiveness of a weight loss program,members are weighed at the beginning and the end of the program.This is an example of independent samples with unequal population variances.

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: n_x = 360, _x = 0.69,n_y = 350, _y = 0.76 -What is the lower confidence limit of the 98% confidence interval for the difference in population proportions?

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: A confidence interval for the difference between the means of two normally distributed populations based on the following dependent samples is desired: 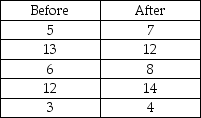-If the observed sample means are and Then a 100(1- α)% confidence interval for the difference between two means,independent samples,and known population variances is given by:

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: In a random sample of 150 large retailers,110 used regression as a method of forecasting.In an independent random sample of 180 small retailers,90 used regression as a method of forecasting. -Find the margin of error for a 90% confidence interval.

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: Independent random sampling from two normally distributed populations gives the following results: n_x = 55, = 520,σ_x = 30,n_y = 45, = 482,and σ_y = 24 -Assuming equal population variances,determine the number of degrees of freedom for the following: n₁ = 18, 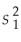= 28;n₂ = 22,and 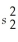= 24

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: For calculating a 95% confidence interval for μ₁ - μ₂ the difference between the means of two normally distributed populations,the summary statistics from two independent samples are: n_x = 60, = 180, 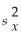= 360,n_y = 45, = 160,and 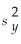= 900. It is assumed that the Population variances are unknown and are equal. -What is the lower confidence limit of the 95% confidence interval?

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: A dependent random sample from two normally distributed populations gives the following results: n = 15, = 20.5,and s_d = 2.4 -Find the margin of error for a 95% confidence interval for the difference in the means of the two populations.

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: Two dependent random samples from two normally distributed populations gives the following results: n = 10; = 20.5;s_d = 3.2 -Find the upper confidence limit of the 95% confidence interval for the difference between the means of the two populations.

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: A dependent random sample from two normally distributed populations gives the following results: n = 20, = 26.5,s₂ = 3.2 -Calculate the margin of error.

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: In a recent survey of 240 teachers in Richmond,Virginia,77.2% supported standardized national testing of elementary students.In a survey of 162 teachers in Raleigh,North Carolina,64.2% supported national testing. -What is the upper confidence limit of the 99% confidence interval for the difference between the two population proportions?

If the population distribution of the differences between means of dependent samples is assumed to be normal,then a 100(1- α)% confidence interval for the difference between two means and dependent samples is given by:

Assuming equal population variances,determine the number of degrees of freedom for the following: n₁ = 16, 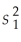= 25;n₂ = 20,and 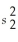= 30

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: In a random sample of 125 large retailers,90 used regression as a method of forecasting.In an independent random sample of 160 small retailers,80 used regression as a method of forecasting. -Based on the 95% confidence interval for the difference between the two population proportions,is there evidence that the population proportions are different?

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: The means and variances are obtained from two independent samples.Assume that the populations from which the samples were drawn have unequal variances. -Determine the number of degrees of freedom for n₁ = 8, 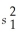= 15,n₂ = 12,and 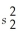= 25.

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: Independent samples of math scores from students in the U.S.and Europe were collected from normal populations.A sample of 50 students from the U.S.had an average score of 570 while a sample of 50 European students had an average score of 540.The population standard deviations for the average scores of the US and European students are 102 and 115 respectively. -What is the upper confidence limit of the 95% confidence interval for the difference between the population means?

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: For constructing a 95% confidence interval estimate for the difference between the means of two normally distributed populations,where the unknown population variances are assumed not to be equal,the summary statistics computed from two independent samples are as follows: n₁ = 50, ₁ = 175,s₁ = 18.5,n₂ = 42, ₂ = 158,and s₂ = 32.4 -What is the upper confidence limit of the 95% confidence interval for the difference between the means?

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: A computer information systems manager was in charge of purchasing new battery packs for laptop computers.The choices were narrowed to two available models.Since the two models cost about the same,the manager was interested in determining whether there was a difference in the average time the battery packs would function before needing to be recharged.Based on two independent random samples,the following summary information was computed: 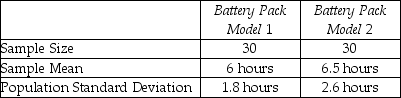-Find a 99% confidence interval for the difference in average functioning time before recharging the two models.

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: The residents of Austin,Texas,complain that parking fines given in their city are higher than the parking fines that are given in Houston.Independent random samples of the amounts paid by residents for parking tickets in each of two cities over the last four months were obtained.Assume the population variances are equal.These amounts were as follows: -What is the mean of the parking fines issued in Houston?

THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION: A confidence interval for the difference between the means of two normally distributed populations based on the following dependent samples is desired: -What is the width of the interval?