Exam 11: Hypothesis Tests and Estimation for Population Variances
Exam 1: The Where, why, and How of Data Collection167 Questions
Exam 2: Graphs,charts and Tablesdescribing Your Data138 Questions
Exam 3: Describing Data Using Numerical Measures130 Questions
Exam 4: Using Probability and Probability Distributions77 Questions
Exam 5: Discrete Probability Distributions119 Questions
Exam 6: Introduction to Continuous Probability Distributions90 Questions
Exam 7: Introduction to Sampling Distributions104 Questions
Exam 8: Estimating Single Population Parameters145 Questions
Exam 9: Introduction to Hypothesis Testing129 Questions
Exam 10: Estimation and Hypothesis Testing for Two Population Parameters97 Questions
Exam 11: Hypothesis Tests and Estimation for Population Variances71 Questions
Exam 12: Analysis of Variance137 Questions
Exam 13: Goodness-Of-Fit Tests and Contingency Analysis104 Questions
Exam 14: Introduction to Linear Regression and Correlation Analysis136 Questions
Exam 15: Multiple Regression Analysis and Model Building153 Questions
Exam 16: Analyzing and Forecasting Time-Series Data133 Questions
Exam 17: Introduction to Nonparametric Statistics104 Questions
Exam 18: Introduction to Quality and Statistical Process Control110 Questions
Exam 19: Introduction to Decision Analysis116 Questions
Select questions type
A one-tailed hypothesis test for a population variance always has the rejection region in the upper tail.
(True/False)
4.8/5  (39)
(39)
In a two-tailed test for the equality of two variances,the critical value is determined by going to the F-distribution table with an upper-tail area equal to alpha divided by two.
(True/False)
4.8/5  (34)
(34)
In a two-tailed hypothesis test for the difference between two population variances,if s1 = 3 and s2 = 5,then the test statistic is F = 2.7778.
(True/False)
4.8/5  (37)
(37)
In a test for determining whether two population variances are the same or different,the larger the sample sizes from the two populations,the lower will be the chance of making a Type I statistical error.
(True/False)
4.9/5  (31)
(31)
When a hypothesis test is to be conducted regarding a population variance,the test statistic will be:
(Multiple Choice)
4.8/5  (28)
(28)
To test the following hypotheses at the 0.05 level of significance,using a sample size of n = 15.  What is the upper tail critical value?
What is the upper tail critical value?
(Multiple Choice)
4.8/5  (35)
(35)
If the variance of the contents of cans of orange juice is significantly more than 0.003,the manager has to order to stop the filling machine.A sample of 26 cans of orange juice showed a standard deviation of 0.06 ounces.Based on the sample and at the 0.05 level of significance,the filling machine should be
(Multiple Choice)
4.8/5  (41)
(41)
A machine that is used to fill soda pop cans with pop has an adjustable mean fill setting,but the standard deviation is not supposed to exceed 0.18 ounces.To make sure that this is the case,the managers at the beverage company each day select a random sample of n = 6 cans and measure the fill volume carefully.In one such case,the following data (ounces per can)were observed.  Based on these sample data,the test statistic is approximately χ2 = 5.01.
Based on these sample data,the test statistic is approximately χ2 = 5.01.
(True/False)
5.0/5  (29)
(29)
The null hypothesis that two population variances are equal will tend to be rejected if the ratio of the sample variances from each population is substantially larger than 1.0.
(True/False)
4.8/5  (38)
(38)
It is believed that the SAT scores for students entering two state universities may have different standard deviations.Specifically,it is believed that the standard deviation at University A is greater than the standard deviation at University B.To test this using an alpha = 0.05 level,a sample of 14 student SAT scores from University A was selected and a sample of 8 SAT scores from University B was selected.The following sample results were observed: 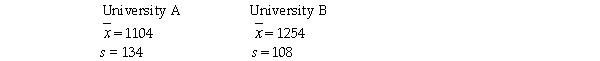 Based on this information,what is the critical value that will be used to test the hypothesis?
Based on this information,what is the critical value that will be used to test the hypothesis?
(Multiple Choice)
4.9/5  (37)
(37)
Showing 61 - 71 of 71
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)