Exam 6: Continuous Probability Distributions

Exhibit 6-5 The travel time for a college student traveling between her home and her college is uniformly distributed between 40 and 90 minutes. -Refer to Exhibit 6-5.The probability that her trip will take exactly 50 minutes is

Exhibit 6-7 The weight of items produced by a machine is normally distributed with a mean of 8 ounces and a standard deviation of 2 ounces. -Refer to Exhibit 6-7.What is the probability that a randomly selected item will weigh between 11 and 12 ounces?

Given that Z is a standard normal random variable,what is the value of Z if the are to the left of Z is 0.0559?

The salaries at a corporation are normally distributed with an average salary of $19,000 and a standard deviation of $4,000. a.What is the probability that an employee will have a salary between $12,520 and $13,480? b.What is the probability that an employee will have a salary more than $11,880? c.What is the probability that an employee will have a salary less than $28,440?

A continuous random variable may assume

Given that Z is a standard normal random variable.What is the value of Z if the area to the left of Z is 0.9382?

X is a normally distributed random variable with a mean of 12 and a standard deviation of 3.The probability that X equals 19.62 is

The weights of the contents of cans of tomato sauce produced by a company are normally distributed with a mean of 8 ounces and a standard deviation of 0.2 ounces. a.What percentage of all cans produced contain more than 8.4 ounces of tomato paste? b.What percentage of all cans produced contain less than 7.8 ounces? c.What percentage of cans contains between 7.4 and 8.2 ounces? d.Ninety-five percent of cans will contain at least how many ounces? e.What percentage of cans contains between 8.2 and 8.4 ounces?

The average starting salary of this year's graduates of a large university (LU)is $20,000 with a standard deviation of $8,000.Furthermore,it is known that the starting salaries are normally distributed. a.What is the probability that a randomly selected LU graduate will have a starting salary of at least $30,400? b.Individuals with starting salaries of less than $15,600 receive a low income tax break.What percentage of the graduates will receive the tax break? c.What are the minimum and the maximum starting salaries of the middle 95% of the LU graduates? d.If 189 of the recent graduates have salaries of at least $32,240,how many students graduated this year from this university?

"DRUGS R US" is a large manufacturer of various kinds of liquid vitamins.The quality control department has noted that the bottles of vitamins marked 6 ounces vary in content with a standard deviation of 0.3 ounces.Assume the contents of the bottles are normally distributed. a.What percentage of all bottles produced contains more than 6.51 ounces of vitamins? b.What percentage of all bottles produced contains less than 5.415 ounces? c.What percentage of bottles produced contains between 5.46 to 6.495 ounces? d.Ninety-five percent of the bottles will contain at least how many ounces? e.What percentage of the bottles contains between 6.3 and 6.6 ounces?

Z is a standard normal random variable.Compute the following probabilities. a.P(-1.33 $\le$ Z1.67) b.P(1.23 $\ge$ Z1.55) c.P(Z $\ge$ 2.32) d.P(Z $\ge$ -2.08) e.P(Z $\le$ -1.08)

Exhibit 6-8 The life expectancy of a particular brand of tire is normally distributed with a mean of 40,000 and a standard deviation of 5,000 miles. -Refer to Exhibit 6-8.What is the probability that a randomly selected tire will have a life of at least 30,000 miles?

Exhibit 6-10 A professor at a local university noted that the grades of her students were normally distributed with a mean of 73 and a standard deviation of 11. -Refer to Exhibit 6-10.The professor has informed us that 7.93 percent of her students received grades of A.What is the minimum score needed to receive a grade of A?

A manufacturing process produces items whose weights are normally distributed.It is known that 22.57% of all the items produced weigh between 100 grams up to the mean and 49.18% weigh from the mean up to 190 grams.Determine the mean and the standard deviation.

The exponential probability distribution is used with

Z is a standard normal random variable.The P (1.20 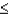Z 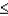1.85)equals

Exhibit 6-2 The weight of football players is normally distributed with a mean of 200 pounds and a standard deviation of 25 pounds. -Refer to Exhibit 6-2.The probability of a player weighing less than 250 pounds is

For a standard normal distribution,determine the probabilities of obtaining the following z values.It is helpful to draw a normal distribution for each case and show the corresponding area. a.Greater than zero b.Between -2.4 and -2.0 c.Less than 1.6 d.Between -1.9 to 1.7 e.Between 1.5 and 1.75

The monthly earnings of computer systems analysts are normally distributed with a mean of $4,300.If only 1.07 percent of the systems analysts have a monthly income of more than $6,140,what is the value of the standard deviation of the monthly earnings of the computer systems analysts?

Exhibit 6-9 The average price of personal computers manufactured by MNM Company is $1,200 with a standard deviation of $220.Furthermore,it is known that the computer prices manufactured by MNM are normally distributed. -Refer to Exhibit 6-9.Computers with prices of more than $1,750 receive a discount.What percentage of the computers will receive the discount?