Exam 13: Introduction to Multiple Regression

Instruction 13.23 The Head of the Accounting Department wanted to see if she could predict the average grade of students using the number of course units (credits) and total university entrance exam scores of each. She takes a sample of students and generates the following Microsoft Excel output: OUTPUT SUMMARY Regression Statistics MultipleR 0.916 R Square 0.839 Adj. R Square 0.732 Std. Error 0.24685 Observations 6 ANOVA df SS MS F Signiff Regression 2 0.95219 0.47610 7.813 0.0646 Residual 3 0.18281 0.06094 Total 5 1.13500 Coeff StdError t Stat p value Intercept 4.593897 1.13374542 4.052 0.0271 GDP -0.247270 0.06268485 -3.945 0.0290 Price 0.001443 0.00101241 1.425 0.2494 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.23,the Head of Department decided to construct a 95% confidence interval for ?₁. The confidence interval is from _____ to _____.

Instruction 13.35 The education department's regional executive officer wanted to predict the percentage of students passing a Grade 6 proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries) and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending: 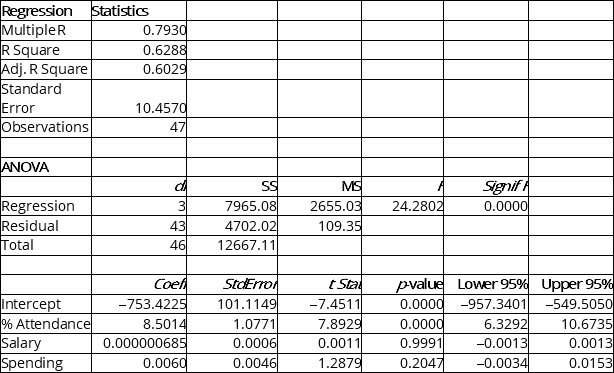-Referring to Instruction 13.35,which of the following is the correct alternative hypothesis to test whether daily mean of the percentage of students attending class has any effect on percentage of students passing the proficiency test,taking into account the effect of all the other independent variables?

AU: Question 37 is the same as Question 36. Please check. Instruction 13.12 AU: Please advise if Instruction 13.12 can be renumbered to Instruction 13.11 and further questions renumbered. Or advise whether there shall be new Instruction 13.11 included. The Head of the Accounting Department wanted to see if she could predict the average grade of students using the number of course units (credits) and total university entrance exam scores of each. She takes a sample of students and generates the following Microsoft Excel output: OUTPUT SUMMARY Regression Statistics MultipleR 0.916 R Square 0.839 Adj. R Square 0.732 Std. Error 0.24685 Observations 6 ANOVA df SS MS F Signiff Regression 2 0.95219 0.47610 7.813 0.0646 Residual 3 0.18281 0.06094 Total 5 1.13500 Coeff StdError t Stat p value Intercept 4.593897 1.13374542 4.052 0.0271 GDP -0.247270 0.06268485 -3.945 0.0290 Price 0.001443 0.00101241 1.425 0.2494 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.12,the estimate of the unit change in the mean of Y per unit change in X₁,holding X₂ constant,is___________.

When an explanatory variable is dropped from a multiple regression model,the adjusted r² can increase.

Instruction 13.25 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. Model 1 Regression Statistics Multiple R 0.7035 R Square 0.4949 Adj. R Square 0.4030 Std. Error 18.4861 Observations 40 ANOVA df SS MS F Signiff Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 223325.9 Coeff StdError tStat p value Lower 95\% Upper95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below: Mode 2 Regression Statistics Multiple R 0.6391 R Square 0.4085 Adj. R Square 0.3765 Std. Error 18.8929 Observations 40 ANOVA df SS MS F Signiff Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coeff StdError t Stat p value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to Instruction 13.25 Model 1,the alternative hypothesis $H _ { 1 }$ : At least one of ?_j ? 0 for j = 1,2,3,4,5,6 implies that the number of weeks a worker is unemployed due to a layoff is related to all of the explanatory variables.

Instruction 13.31 A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. The Microsoft Excel output below shows results of this multiple regression. 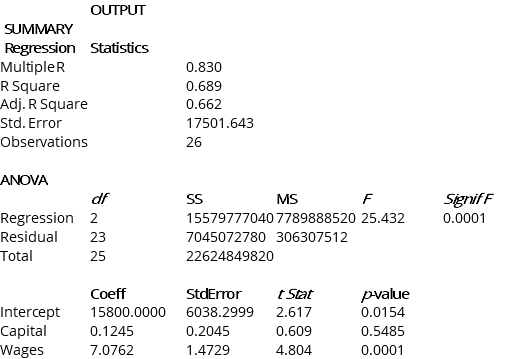Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.31,what is the p-value for Wages?

Instruction 13.22 The education department's regional executive officer wanted to predict the percentage of students passing a Grade 6 proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries) and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending: 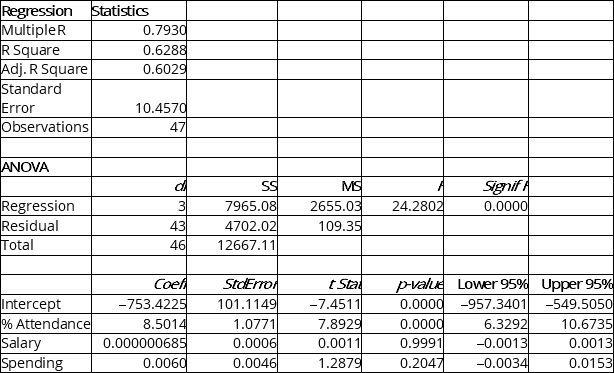-Referring to Instruction 13.22,which of the following is a correct statement?

Instruction 13.3 An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index). The Microsoft Excel output of this regression is partially reproduced below. OUTPUT SUMMARY Regression Statistics MultipleR 0.991 R Square 0.982 Adj. R Square 0.976 Std. Error 0.299 Observations 10 ANOVA df SS MS F Signif F Regression 2 33.4163 16.7082 186.325 0.0001 Residual 7 0.6277 0.0897 Total 9 34.0440 Coeff StdError t Stat p value Intercept -1.6335 0.5674 -0.152 0.8837 GDP 0.7654 0.0574 13.340 0.0001 Price -0.0006 0.0028 -0.219 0.8330 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.3,the p-value for the regression model as a whole is

An interaction term in a multiple regression model may be used when

Instruction 13.41 An automotive engineer would like to be able to predict automobile fuel economy. She believes that the two most important characteristics that affect economy are engine power and the number of cylinders (4 or 6) of a car. She believes that the appropriate model is Y=40-0.05+20-0.1 where = engine power =1 if 4 cylinders, 0 if 6 cylinders Y = economy expressed as kilometres. -Referring to Instruction 13.41,the fitted model for predicting economy for 6-cylinder cars is______.

Instruction 13.22 The education department's regional executive officer wanted to predict the percentage of students passing a Grade 6 proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries) and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending: -Referring to Instruction 13.22,the null hypothesis H₀: β₁ = β₂ = β₃= 0 implies that percentage of students passing the proficiency test is not affected by some of the explanatory variables.

Instruction 13.25 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. Model 1 Regression Statistics Multiple R 0.7035 R Square 0.4949 Adj. R Square 0.4030 Std. Error 18.4861 Observations 40 ANOVA df SS MS F Signiff Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 223325.9 Coeff StdError tStat p value Lower 95\% Upper95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below: Mode 2 Regression Statistics Multiple R 0.6391 R Square 0.4085 Adj. R Square 0.3765 Std. Error 18.8929 Observations 40 ANOVA df SS MS F Signiff Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coeff StdError t Stat p value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to Instruction 13.25 Model 1,you can conclude that,holding constant the effect of the other independent variables,the number of years of education received has no impact on the mean number of weeks a worker is unemployed due to a layoff at a 10% level of significance if all you have is the information on the 95% confidence interval estimate for ?₂.

Instruction 13.1 A manager of a product sales group believes the number of sales made by an employee (Y) depends on how many years that employee has been with the company (X₁) and how he/she scored on a business aptitude test (X₂). A random sample of 8 employees provides the following: Employee Y X1 X2 1 100 10 7 2 90 3 10 3 80 8 9 4 70 5 4 5 60 5 8 6 50 7 5 7 40 1 4 8 30 1 1 -Referring to Instruction 13.1,for these data,what is the estimated coefficient for the variable representing years an employee has been with the company,b₁?

Instruction 13.16 A real estate builder wishes to determine how house size (House) is influenced by family income (Income), family size (Size) and education of the head of household (School). House size is measured in hundreds of square metres, income is measured in thousands of dollars and education is in years. The builder randomly selected 50 families and ran the multiple regression. Microsoft Excel output is provided below: OUTPUT SUMMARY Regression Statistics Multiple R 0.865 R Square 0.748 Adj. R Square 0.726 Std. Error 5.195 Observations 50 ANOVA df SS MS F Signiff Regression 3605.7736 901.4434 0.0001 Residual 1214.2264 26.9828 Total 49 4820.0000 Coeff StdError t Stat p value Intercept -1.6335 5.8078 -0.281 0.7798 Income 0.4485 0.1137 3.9545 0.0003 Size 4.2615 0.8062 5.286 0.0001 School -0.6517 0.4319 -1.509 0.1383 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.16,what are the residual degrees of freedom that are missing from the output?

Instruction 13.38 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in kilograms). Two variables thought to effect weight-loss are client's length of time on the weight loss program and time of session. These variables are described below: $Y =$ Weight-loss (in kilograms) $X _ { 1 } =$ Length of time in weight-loss program (in months) $x _ { 2 } = 1$ if morning session, 0 if not $x _ { 3 } = 1$ if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: $Y = \beta 0 + \beta _ { 1 } X _ { 1 } + \beta _ { 2 } X _ { 2 } + \beta _ { 3 } X _ { 3 } + \beta _ { 4 } X _ { 1 } X _ { 2 } + \beta _ { 5 } X _ { 1 } X _ { 3 } + \varepsilon$ Partial output from Microsoft Excel follows: 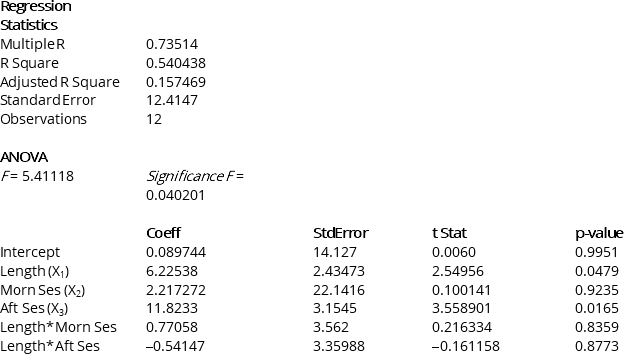-Referring to Instruction 13.38,in terms of the ?s in the model,give the mean change in weight-loss (Y)for every 1 month increase in time in the program (X₁)when attending the afternoon session.

Instruction 13.7 You worked as an intern at We Always Win Car Insurance Company last summer. You notice that individual car insurance premium depends very much on the age of the individual, the number of traffic tickets received by the individual and the population density of the city in which the individual lives. You performed a regression analysis in Microsoft Excel and obtained the following information: Regression Analysis MultipleR 0.63 R Square 0.40 Adj. R Square 0.23 Standard Error 50.00 Observations 15.00 ANOVA df SS MS F Signif F Regression 3 5994.24 2.40 0.12 Residual 11 27496.82 Total 45479.54 Coeff StdError t Stat p-value Lower 99.0\% Upper 99.0\% Intercept 123.80 48.71 2.54 0.03 -27.47 275.07 AGE 0.82 0.87 -0.95 0.36 -3.51 1.87 TICKETS 11.25 10.66 1.99 0.07 -11.86 54.37 DENSITY -3.14 6.46 -0.49 0.64 -23.19 16.91 -Referring to Instruction 13.7,the total degrees of freedom that are missing in the ANOVA table should be ___________.

Instruction 13.38 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in kilograms). Two variables thought to effect weight-loss are client's length of time on the weight loss program and time of session. These variables are described below: $Y =$ Weight-loss (in kilograms) $X _ { 1 } =$ Length of time in weight-loss program (in months) $x _ { 2 } = 1$ if morning session, 0 if not $x _ { 3 } = 1$ if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: $Y = \beta 0 + \beta _ { 1 } X _ { 1 } + \beta _ { 2 } X _ { 2 } + \beta _ { 3 } X _ { 3 } + \beta _ { 4 } X _ { 1 } X _ { 2 } + \beta _ { 5 } X _ { 1 } X _ { 3 } + \varepsilon$ Partial output from Microsoft Excel follows: -Referring to Instruction 13.38,in terms of the ?s in the model,give the mean change in weight-loss (Y)for every 1 month increase in time in the program (X₁)when attending the evening session.

Instruction 13.1 A manager of a product sales group believes the number of sales made by an employee (Y) depends on how many years that employee has been with the company (X₁) and how he/she scored on a business aptitude test (X₂). A random sample of 8 employees provides the following: Employee Y X1 X2 1 100 10 7 2 90 3 10 3 80 8 9 4 70 5 4 5 60 5 8 6 50 7 5 7 40 1 4 8 30 1 1 -Referring to Instruction 13.1,for these data,what is the estimated coefficient for the variable representing scores on the aptitude test,b₂?

To explain personal consumption (CONS)measured in dollars,data is collected for INC: personal income in dollars CRDTLIM: \ 1 plus the credit limit in dollars available to the individual APR: average annualised percentage interest rate for borrowing for the individual per person advertising expenditure in dollars by manufacturersin the city ADVT: where the individuallives GENDER: gender of the individual; 1 if female, 0 if male A regression analysis was performed with CONS as the dependent variable and log(CRDTLIM),ln(APR),log(ADVT)and GENDER as the independent variables.The estimated model was $\hat{y}$ = 2.28 * 0.29 log(CRDTLIM)+ 5.77 llogAPR)+ 2.35 log(ADVT)+ 0.39 GENDER AU: Please advise if 'llogAPR' is 'logAPR'. What is the correct interpretation for the estimated coefficient for GENDER?

Instruction 13.25 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. Model 1 Regression Statistics Multiple R 0.7035 R Square 0.4949 Adj. R Square 0.4030 Std. Error 18.4861 Observations 40 ANOVA df SS MS F Signiff Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 223325.9 Coeff StdError tStat p value Lower 95\% Upper95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below: Mode 2 Regression Statistics Multiple R 0.6391 R Square 0.4085 Adj. R Square 0.3765 Std. Error 18.8929 Observations 40 ANOVA df SS MS F Signiff Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coeff StdError t Stat p value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to Instruction 13.25 Model 1,there is sufficient evidence that all of the explanatory variables are related to the number of weeks a worker is unemployed due to a layoff at a 10% level of significance.