Exam 13: Introduction to Multiple Regression

Instruction 13.13 A financial analyst wanted to examine the relationship between salary (in $1,000) and four variables: age (X₁ = Age), experience in the field (X₂ = Exper), number of degrees (X₃ = Degrees) and number of previous jobs in the field (X₄ = Prevjobs). He took a sample of 20 employees and obtained the following Microsoft Excel output: $\text { OUTPUT }$ SUMMARY Regression Statistics Multiple R 0.992 R Square 0.984 Adj. R Square 0.979 Std. Error 2.26743 Observations 20 ANOVA df SS MS F Signif F Regression 4 4609.83164 1152.45791 224.160 0.0001 Residual 15 77.11836 5.14122 Total 19 4686.95000 Coeff Std Error t Stat p value Intercept -9.611198 2.77988638 -3.457 0.0035 Age 1.327695 0.11491930 11.553 0.0001 Exper -0.106705 0.14265559 -0.748 0.4660 Degrees 7.311332 0.80324187 9.102 0.0001 Prevjobs -0.504168 0.44771573 -1.126 0.2778 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.13,the estimate of the unit change in the mean of Y per unit change in X₄,taking into account the effects of the other three variables,is ___________.

Instruction 13.23 The Head of the Accounting Department wanted to see if she could predict the average grade of students using the number of course units (credits) and total university entrance exam scores of each. She takes a sample of students and generates the following Microsoft Excel output: OUTPUT SUMMARY Regression Statistics MultipleR 0.916 R Square 0.839 Adj. R Square 0.732 Std. Error 0.24685 Observations 6 ANOVA df SS MS F Signiff Regression 2 0.95219 0.47610 7.813 0.0646 Residual 3 0.18281 0.06094 Total 5 1.13500 Coeff StdError t Stat p value Intercept 4.593897 1.13374542 4.052 0.0271 GDP -0.247270 0.06268485 -3.945 0.0290 Price 0.001443 0.00101241 1.425 0.2494 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.23,the Head of Department wants to use a t test to test for the significance of the coefficient of X₁.For a level of significance of 0.05,the critical values of the test are _____.

Instruction 13.22 The education department's regional executive officer wanted to predict the percentage of students passing a Grade 6 proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries) and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending: 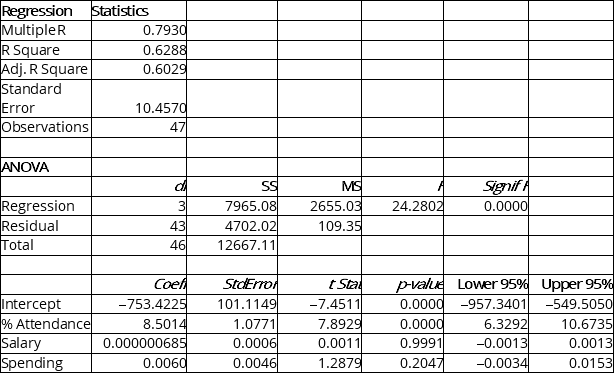-Referring to Instruction 13.22,what is the p-value of the test statistic to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?

Instruction 13.22 The education department's regional executive officer wanted to predict the percentage of students passing a Grade 6 proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries) and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending: -Referring to Instruction 13.22,the null hypothesis should be rejected at a 5% level of significance when testing whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables.

Instruction 13.7 You worked as an intern at We Always Win Car Insurance Company last summer. You notice that individual car insurance premium depends very much on the age of the individual, the number of traffic tickets received by the individual and the population density of the city in which the individual lives. You performed a regression analysis in Microsoft Excel and obtained the following information: Regression Analysis MultipleR 0.63 R Square 0.40 Adj. R Square 0.23 Standard Error 50.00 Observations 15.00 ANOVA df SS MS F Signif F Regression 3 5994.24 2.40 0.12 Residual 11 27496.82 Total 45479.54 Coeff StdError t Stat p-value Lower 99.0\% Upper 99.0\% Intercept 123.80 48.71 2.54 0.03 -27.47 275.07 AGE 0.82 0.87 -0.95 0.36 -3.51 1.87 TICKETS 11.25 10.66 1.99 0.07 -11.86 54.37 DENSITY -3.14 6.46 -0.49 0.64 -23.19 16.91 -Referring to Instruction 13.7,to test the significance of the multiple regression model,the value of the test statistic is ___________.

Instruction 13.37 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. Model 1 Regression Statistics Multiple R 0.7035 R Square 0.4949 Adj. R Square 0.4030 Std. Error 18.4861 Observations 40 ANOVA df SS MS F Signif F Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 223325.9 Coeff StdError tStat p value Lower 95\% Upper95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below: Mode 2 Regression Statistics Multiple R 0.6391 R Square 0.4085 Adj. R Square 0.3765 Std. Error 18.8929 Observations 40 ANOVA df SS MS F Signif F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coeff StdError t Stat p value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to Instruction 13.37 Model 1,there is sufficient evidence that age has an effect on the number of weeks a worker is unemployed due to a layoff,while holding constant the effect of all the other independent variables at a 10% level of significance.

Instruction 13.21 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in kilograms). Two variables thought to effect weight-loss are client's length of time on the weight loss program and time of session. These variables are described below: Y = Weight-loss (in kilograms) X₁ = Length of time in weight-loss program (in months) X₂ = 1 if morning session, 0 if not X₃ = 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: Y = β0 + β₁X₁ + β₂X₂ + β₃X₃ + β₄X₁X₂ + β₅X₁X₃ + ε Partial output from Microsoft Excel follows: 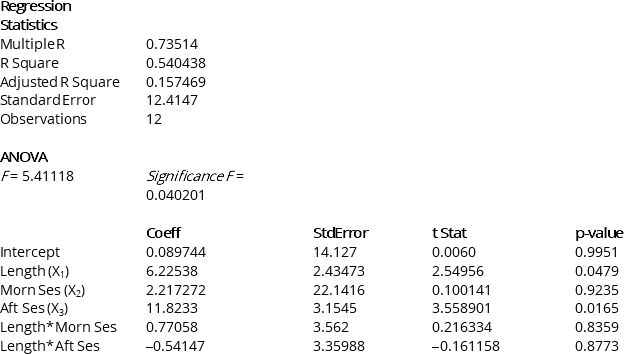-In a multiple regression model,the adjusted r²

Instruction 13.22 The education department's regional executive officer wanted to predict the percentage of students passing a Grade 6 proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries) and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending: -Referring to Instruction 13.22,you can conclude that mean teacher salary has no impact on mean percentage of students passing the proficiency test at a 1% level of significance based solely on the 95% confidence interval estimate for β₂.

Instruction 13.35 The education department's regional executive officer wanted to predict the percentage of students passing a Grade 6 proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries) and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X₁ = % Attendance, X₂ = Salaries and X₃ = Spending: 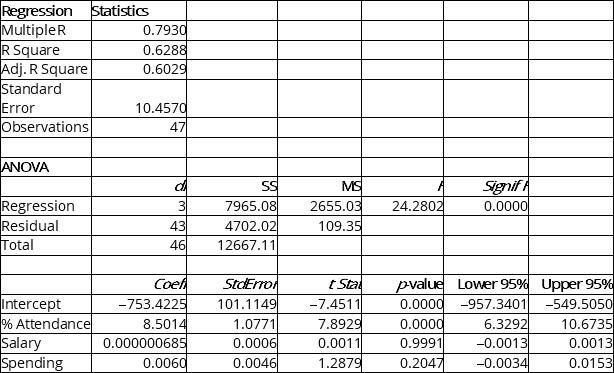-Referring to Instruction 13.35,which of the following is the correct alternative hypothesis to test whether instructional spending per pupil has any effect on percentage of students passing the proficiency test,taking into account the effect of all the other independent variables?

In trying to obtain a model to estimate grades on a statistics test,a lecturer wanted to include,among other factors,whether the person had taken the course previously.To do this,the lecturer included a dummy variable in her regression that was equal to 1 if the person had previously taken the course,and 0 otherwise.The interpretation of the coefficient associated with this dummy variable would be the mean amount the repeat students tended to be above or below non-repeaters,with all other factors the same.

A dummy variable is used as an independent variable in a regression model when

Instruction 13.16 A real estate builder wishes to determine how house size (House) is influenced by family income (Income), family size (Size) and education of the head of household (School). House size is measured in hundreds of square metres, income is measured in thousands of dollars and education is in years. The builder randomly selected 50 families and ran the multiple regression. Microsoft Excel output is provided below: OUTPUT SUMMARY Regression Statistics Multiple R 0.865 R Square 0.748 Adj. R Square 0.726 Std. Error 5.195 Observations 50 ANOVA df SS MS F Signiff Regression 3605.7736 901.4434 0.0001 Residual 1214.2264 26.9828 Total 49 4820.0000 Coeff StdError t Stat p value Intercept -1.6335 5.8078 -0.281 0.7798 Income 0.4485 0.1137 3.9545 0.0003 Size 4.2615 0.8062 5.286 0.0001 School -0.6517 0.4319 -1.509 0.1383 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.16,when the builder used a simple linear regression model with house size (House)as the dependent variable and education (School)as the independent variable,he obtained an r² value of 23.0%.What additional percentage of the total variation in house size has been explained by including family size and income in the multiple regression?

Instruction 13.29 An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index). The Microsoft Excel output of this regression is partially reproduced below. OUTPUT SUMMARY Regression Statistics MultipleR 0.991 R Square 0.982 Adj. R Square 0.976 Std. Error 0.299 Observations 10 ANOVA df SS MS F Signiff Regression 2 33.4163 16.7082 186.325 0.0001 Residual 7 0.6277 0.0897 Total 9 34.0440 Coeff StdError t Stat p value Intercept -1.6335 0.5674 -0.152 0.8837 GDP 0.7654 0.0574 13.340 0.0001 Price -0.0006 0.0028 -0.219 0.8330 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.29,to test whether gross domestic product has a positive impact on consumption,the p-value is

The potential for correlation within a set of independent X variables is known as ______.

Instruction 13.27 A real estate builder wishes to determine how house size (House) is influenced by family income (Income), family size (Size) and education of the head of household (School). House size is measured in hundreds of square metres, income is measured in thousands of dollars and education is in years. The builder randomly selected 50 families and ran the multiple regression. Microsoft Excel output is provided below: OUTPUT SUMMARY Regression Statistics Multiple R 0.865 R Square 0.748 Adj. R Square 0.726 Std. Error 5.195 Observations 50 ANOVA df SS MS F Signiff Regression 3605.7736 901.4434 0.0001 Residual 1214.2264 26.9828 Total 49 4820.0000 Coeff StdError t Stat p value Intercept -1.6335 5.8078 -0.281 0.7798 Income 0.4485 0.1137 3.9545 0.0003 Size 4.2615 0.8062 5.286 0.0001 School -0.6517 0.4319 -1.509 0.1383 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.27,one individual in the sample had an annual income of $10,000,a family size of 1 and an education of 8 years.This individual owned a home with an area of 1,000 square metre (House = 10.00).What is the residual (in hundreds of square metre)for this data point?

Instruction 13.9 As a project for his business statistics class, a student examined the factors that determined parking meter rates throughout the campus area. Data were collected for the price per hour of parking, number of city blocks to the centre of the university and one of the three jurisdictions: on campus, in the CBD and off campus or outside of the CBD and off campus. The population regression model hypothesised is: Yi = ? + ?₁x_1i + ?₂x_2i + ?₃x_2i + ?_i Where Y is the meter price x₁ is the number of blocks to the centre of the university x₂ is a dummy variable that takes the value 1 if the meter is located in the CBD and off campus and the value 0 otherwise x₃ is a dummy variable that takes the value 1 if the meter is located outside of the CBD and off campus, and the value 0 otherwise The following Excel results are obtained: Regression Statistics Multiple R 0.9659 R Square 0.9331 Adj. R Square 0.9294 Standard Error 0.0327 Observations 58 ANOVA d SS F Signif F Regression 3 0.8094 0.2698 251.1995 0.0000 Residual 54 0.058 0.0010 Total 57 0.8675 Coef Stol Error t Stat p -value Intercept 0.5118 0.013 37.4675 2.4904 -0.0045 0.0034 -1.3276 0.1898 -0.2392 0.0123 -19.3942 0.0000 -0.0002 0.0123 -0.0214 0.9829 -Referring to Instruction 13.9,predict the meter rate per hour if one parks outside of the CBD and off campus three blocks from the centre of the university.

Instruction 13.13 A financial analyst wanted to examine the relationship between salary (in $1,000) and four variables: age (X₁ = Age), experience in the field (X₂ = Exper), number of degrees (X₃ = Degrees) and number of previous jobs in the field (X₄ = Prevjobs). He took a sample of 20 employees and obtained the following Microsoft Excel output: $\text { OUTPUT }$ SUMMARY Regression Statistics Multiple R 0.992 R Square 0.984 Adj. R Square 0.979 Std. Error 2.26743 Observations 20 ANOVA df SS MS F Signif F Regression 4 4609.83164 1152.45791 224.160 0.0001 Residual 15 77.11836 5.14122 Total 19 4686.95000 Coeff Std Error t Stat p value Intercept -9.611198 2.77988638 -3.457 0.0035 Age 1.327695 0.11491930 11.553 0.0001 Exper -0.106705 0.14265559 -0.748 0.4660 Degrees 7.311332 0.80324187 9.102 0.0001 Prevjobs -0.504168 0.44771573 -1.126 0.2778 Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.13,the value of the F statistic for testing the significance of the entire regression is ___________.

Instruction 13.28 A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies. She proceeds to randomly select 26 large corporations and record information in millions of dollars. The Microsoft Excel output below shows results of this multiple regression. Note: Adj. R Square = Adjusted R Square; Std. Error = Standard Error -Referring to Instruction 13.28,one company in the sample had sales of $21.439 billion (Sales = 21,439).This company spent $300 million on capital and $700 million on wages.What is the residual (in millions of dollars)for this data point?

Instruction 13.37 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. Model 1 Regression Statistics Multiple R 0.7035 R Square 0.4949 Adj. R Square 0.4030 Std. Error 18.4861 Observations 40 ANOVA df SS MS F Signif F Regression 6 11048.6415 1841.4402 5.3885 0.00057 Residual 33 11277.2586 341.7351 Total 39 223325.9 Coeff StdError tStat p value Lower 95\% Upper95\% Intercept 32.6595 23.18302 1.4088 0.1683 -14.5067 79.8257 Age 1.2915 0.3599 3.5883 0.0011 0.5592 2.0238 Edu -1.3537 1.1766 -1.1504 0.2582 -3.7476 1.0402 Job Yr 0.6171 0.5940 1.0389 0.3064 -0.5914 1.8257 Married -5.2189 7.6068 -0.6861 0.4974 -20.6950 10.2571 Head -14.2978 7.6479 -1.8695 0.0704 -29.8575 1.2618 Manager -24.8203 11.6932 -2.1226 0.0414 -48.6102 -1.0303 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below: Mode 2 Regression Statistics Multiple R 0.6391 R Square 0.4085 Adj. R Square 0.3765 Std. Error 18.8929 Observations 40 ANOVA df SS MS F Signif F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coeff StdError t Stat p value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to Instruction 13.37 Model 1,which of the following is the correct null hypothesis to test whether being married or not makes a difference in the mean number of weeks a worker is unemployed due to a layoff,while holding constant the effect of all the other independent variables?

The interpretation of the slope is different in a multiple linear regression model as compared to a simple linear regression model.