Exam 3: Modeling and Solving Lp Problems in a Spreadsheet
Exam 1: Introduction to Modeling and Decision Analysis74 Questions
Exam 2: Introduction to Optimization and Linear Programming73 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet75 Questions
Exam 4: Sensitivity Analysis and the Simplex Method77 Questions
Exam 5: Network Modeling84 Questions
Exam 6: Integer Linear Programming88 Questions
Exam 7: Goal Programming and Multiple Objective Optimization65 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization69 Questions
Exam 9: Regression Analysis82 Questions
Exam 10: Data Mining102 Questions
Exam 11: Time Series Forecasting81 Questions
Exam 12: Introduction to Simulation Using Analytic Solver Platform70 Questions
Exam 13: Queuing Theory87 Questions
Exam 14: Decision Analysis116 Questions
Exam 15: Project Management Online65 Questions
Select questions type
A company needs to purchase several new machines to meet its future production needs.It can purchase three different types of machines A,B,and C.Each machine A costs $80,000 and requires 2,000 square feet of floor space.Each machine B costs $50,000 and requires 3,000 square feet of floor space.Each machine C costs $40,000 and requires 5,000 square feet of floor space.The machines can produce 200,250 and 350 units per day respectively.The plant can only afford $500,000 for all the machines and has at most 20,000 square feet of room for the machines.The company wants to buy as many machines as possible to maximize daily production.
What values would you enter in the Risk Solver Platform RSP)task pane for the following cells for this Excel spreadsheet implementation of the formulation for this problem?
Objective Cell: Variables Cells: Constraints Cells:
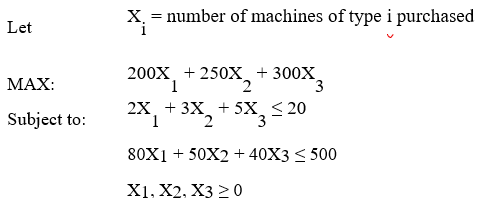
(Essay)
4.8/5  (33)
(33)
The "Analyze Without Solving" tool in Analytic Solver Platform is useful for
(Multiple Choice)
4.8/5  (37)
(37)
What function is used to add the contents of cells A1,A2 and A3?
(Multiple Choice)
4.9/5  (36)
(36)
Exhibit 3.1
The following questions are based on this problem and accompanying Excel windows.
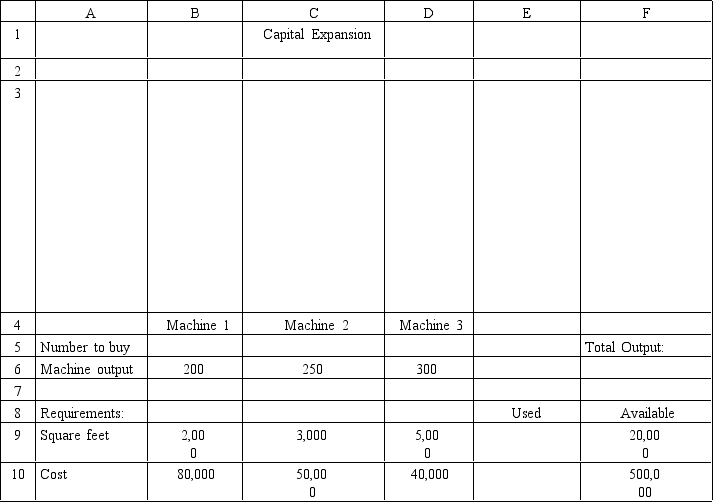
Jones Furniture Company produces beds and desks for college students.The production process requires carpentry and varnishing.Each bed requires 6 hours of carpentry and 4 hour of varnishing.Each desk requires 4 hours of carpentry and 8 hours of varnishing.There are 36 hours of carpentry time and 40 hours of varnishing time available.Beds generate $30 of profit and desks generate $40 of profit.Demand for desks is limited,so at most 8 will be produced.
Let X1 = Number of Beds to produce X2 = Number of Desks to produce
The LP model for the problem is
MAX: 30 X1 + 40 X2
Subject to: 6 X1 + 4 X2 ≤ 36 carpentry)
4 X1 + 8 X2 ≤ 40 varnishing)
X2 ≤ 8 demand for desks)
X1,X2 ≥ 0
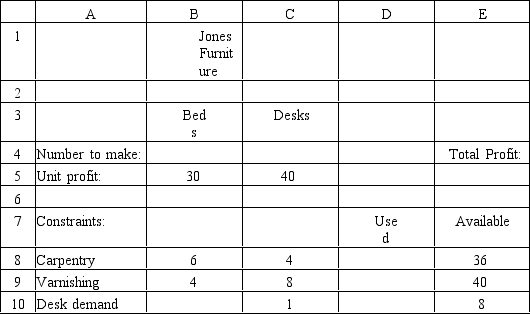 -You have been given the following linear programming model.
MAX: 8 X1 + 5 X2
Subject to: 3 X1 + 5 X2 = 54
11 X1 + 10 X2 ≤ 144 X1 / X2 ≥12
X1,X2 ≥ 0
This formulation:
-You have been given the following linear programming model.
MAX: 8 X1 + 5 X2
Subject to: 3 X1 + 5 X2 = 54
11 X1 + 10 X2 ≤ 144 X1 / X2 ≥12
X1,X2 ≥ 0
This formulation:
(Multiple Choice)
4.8/5  (37)
(37)
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
• homework can account for up to 25% of the grade,but must be at least 5% of the grade;
• the project can account for up to 25% of the grade,but must be at least 5% of the grade;
• the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
• the project and final exam grades may not collectively constitute more than 50% of the grade.Formulate an LP model for Robert to maximize his numerical grade.
(Essay)
4.9/5  (33)
(33)
Pete's Plastics manufactures plastic at plants in Miami,St.Louis and Cleveland.Pete needs to ship plastic to customers in Pittsburgh,Atlanta and Chicago.He wants to minimize the cost of shipping the plastic from his plants to his customers.The data for the problem is summarized in the following table.
Distance From Plants to Customers
Plant Pittsburgh Atlanta Chicago Supply Miani 1,200 700 1,300 30 St. Lauis 700 550 300 40 Cleveland 125 675 350 50 Damand 40 60 20
Formulate the LP for this problem.
(Essay)
4.7/5  (40)
(40)
What action is required to make Analytic Solver Platform ASP)solve a specified problem?
(Multiple Choice)
4.8/5  (40)
(40)
Project 3.1 − The Diet Problem: Ordering Meals from McDonald's
Based on: Robert A.Bosch,"Big Mac Attack: The Diet Problem revisited,Eating at McDonald's," OR/MS Today,
August 1993,pp 30-31.
Tina Simpson is a new fourth-grade teacher at Forest Ridge Elementary.The first teacher workshop for the upcoming school year is next Monday and by majority vote,McDonald's was selected as the food of choice.As the new person,Tina is tasked with developing the meal for the workshop.McDonald's has graciously offered to deliver whatever food Tina decides to order,along with a variety of condiments applicable to whatever is ordered.Rather than offer a menu choice,Tina has decided to simply order the same meal for each person in the workshop.
To get started,Tina took a trip to McDonald's and obtained their published information on the nutritional content of their food.That data is summarized in the table below.
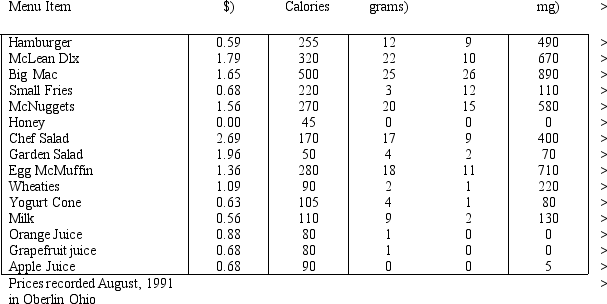
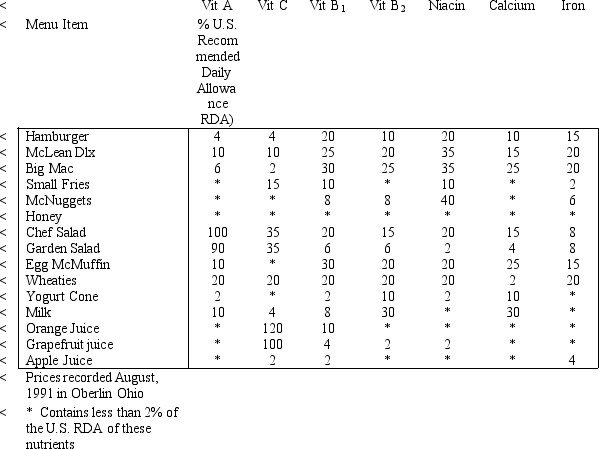 Tina wants the meal to be nutritionally complete.The National Research Council publishes their Recommended Daily Allowances.In this publication,they contend that a diet in this case the meal)should provide at least 100 percent of the U.S.RDA of numerous nutrients.The specific amount of the RDA depends on such factors as age,weight and gender.In addition,the council recommends daily sodium and cholesterol intakes be kept to at most 2.4 grams of sodium and 300 milligrams of cholesterol.Further,at most 30 percent of the calories consumed should come from fat,and at most 10 percent from saturated fat.Each gram of fat contains 9 calories.
Based on the above information,Tina wants to design a least-cost meal that provides at least 100% of the U.S.RDA of vitamins A,C,B1,B2,niacin,calcium,and iron;supplies at least 55 grams of protein;contains at most 3 grams of sodium;and contains at most 30 percent of its calories from fat.Only those foods list in the table above are available for the meal.
Formulate the LP model for Tina's problem.Develop a spreadsheet model of the problem and use Excel Solver to determine the least-cost meal that meets all the stated requirements.
What is the recommended meal? Is this meal reasonable? If not,modify the model to obtain what you believe to be a reasonable meal that meets the stated requirements.
Tina wants the meal to be nutritionally complete.The National Research Council publishes their Recommended Daily Allowances.In this publication,they contend that a diet in this case the meal)should provide at least 100 percent of the U.S.RDA of numerous nutrients.The specific amount of the RDA depends on such factors as age,weight and gender.In addition,the council recommends daily sodium and cholesterol intakes be kept to at most 2.4 grams of sodium and 300 milligrams of cholesterol.Further,at most 30 percent of the calories consumed should come from fat,and at most 10 percent from saturated fat.Each gram of fat contains 9 calories.
Based on the above information,Tina wants to design a least-cost meal that provides at least 100% of the U.S.RDA of vitamins A,C,B1,B2,niacin,calcium,and iron;supplies at least 55 grams of protein;contains at most 3 grams of sodium;and contains at most 30 percent of its calories from fat.Only those foods list in the table above are available for the meal.
Formulate the LP model for Tina's problem.Develop a spreadsheet model of the problem and use Excel Solver to determine the least-cost meal that meets all the stated requirements.
What is the recommended meal? Is this meal reasonable? If not,modify the model to obtain what you believe to be a reasonable meal that meets the stated requirements.
(Not Answered)
This question doesn't have any answer yet
A company is planning production for the next 4 quarters.They want to minimize the cost of production.The production cost,demand and production capacity vary from quarter to quarter.The maximum amount of inventory which can be held is 100 units and management wants to keep at least 50 units on hand.Quarterly inventory holding cost is 4% of the cost of production.There are currently 50 units in inventory.The company wants to produce at no less than one half of its maximum capacity in any quarter.
Quarter
1 2 3 4 Unit Praduction Cost \ 55 \ 50 \ 50 \ 45 Units Demanded 100 150 180 120 Maramum Production 150 150 160 130 Holding cost \ 2.2 \ 2 \ 2 \ 1.8
Let Pi = number of units produced in quarter i,i = 1,... ,4 Bi = beginning inventory for quarter i
MIN: 55 P1 + 50 P 2 + 50 P3 + 45 P4 +
2.2 B1 + B2)/2 + 2 B2 + B3)/2 + 2 B3 + B4)/2 + 1.8 B4 + B5)/2
Subject to: 75 ? P1 ? 150
75 ? P2 ? 150
80 ? P3 ? 160
65 ? P4 ? 130
50 ? B1 + P1 ? 100 ? 100
50 ? B2 + P2 ? 150 ? 100
50 ? B3 + P3 ? 180 ? 100
50 ? B4 + P4 ? 120 ? 100
B2 = B1 + P1 ? 100
B3 = B2 + P2 ? 150
B4 = B3 + P3 ? 180
B5 = B4 + P4 ? 120
Pi,Bi ? 0
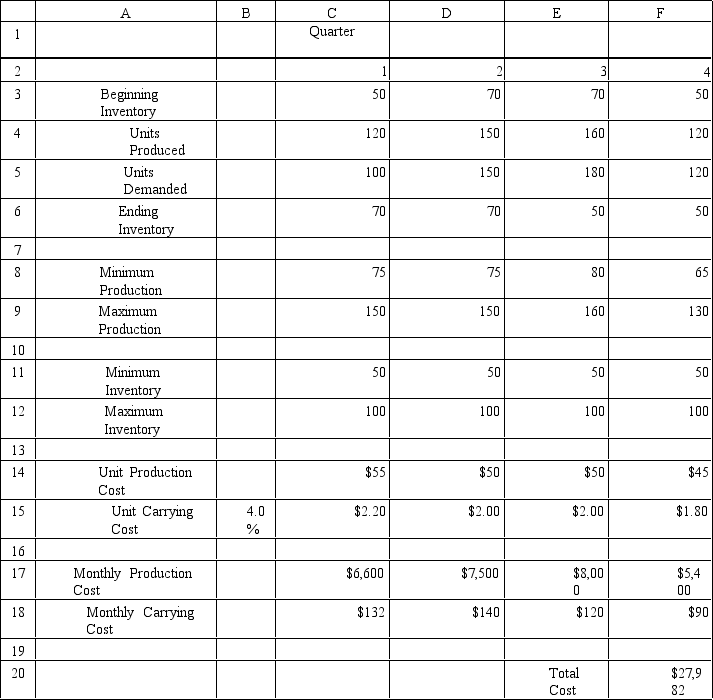 What formulas are required for cells D3,D6,D8,D15,D17 and D18 in the Excel spreadsheet implementation of the formulation?
What formulas are required for cells D3,D6,D8,D15,D17 and D18 in the Excel spreadsheet implementation of the formulation?
(Essay)
4.7/5  (30)
(30)
In the Analytic Solver Platform dialog box simple upper and lower bounds for decision variables are specified by
(Multiple Choice)
4.8/5  (42)
(42)
Exhibit 3.3
The following questions are based on this problem and accompanying Excel windows.
Jack's distillery blends scotches for local bars and saloons.One of his customers has requested a special blend of scotch targeted as a bar scotch.The customer wants the blend to involve two scotch products,call them A and B.Product A is a higher quality scotch while product B is a cheaper brand.The customer wants to make the claim the blend is closer to high quality than the alternative.The customer wants 50 1500 ml bottles of the blend.Each bottle must contain at least 48% of Product A and at least 500 ml of B.The customer also specified that the blend have an alcohol content of at least 85%.Product A contains 95% alcohol while product B contains 78%.The blend is sold for $12.50 per bottle.Product A costs $7 per liter and product B costs $3 per liter.The company wants to determine the blend that will meet the customer's requirements and maximize profit.
Let X1 = Number of liters of product A in total blend delivered X2 = Number of liters of product B in total blend delivered
MIN: 7 X1 + 3 X2
Subject to: X1 + X2 = 1.5 * 50 Total liters of mix)X1 ≥ 0.48 * 1.5 * 50 X1 minimum)
X2 ≥ 0.5 * 50 X2 minimum)
.0.95 X1 + 0.78 X2 ≥ 0.85 * 1.5 * 50 85% alcohol minimum)X1,X2 ≥ 0
A 1 Jacks' Distill ery 2 3 4 Liters to use Total Cost: 5 Unit cost: 10.5 4 6 5 7 Constraints: Supplied Requirement Total Liters 1 1 75 9 A required 1 36 1 B required 1 25 0 1 85\% alcohal 0.95 0.78 63.7 1
-Refer to Exhibit 3.3.What formula should be entered in cell E5 in the accompanying Excel spreadsheet to compute total cost?
(Multiple Choice)
4.8/5  (32)
(32)
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
• homework can account for up to 25% of the grade,but must be at least 5% of the grade;
• the project can account for up to 25% of the grade,but must be at least 5% of the grade;
• the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
• the project and final exam grades may not collectively constitute more than 50% of the grade.The following LP model allows Robert to maximize his numerical grade.
Let W1= weight assigned to homework W2= weight assigned to the project W3= weight assigned to the mid-term
W4= weight assigned to the final

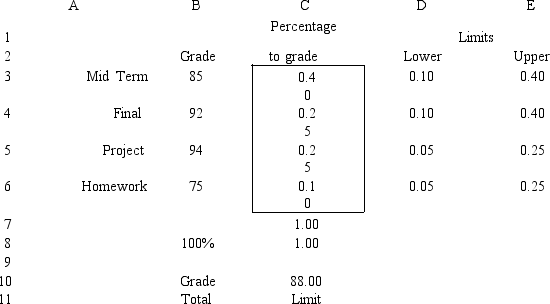 12 Both Exams 0.65 0.70
13 Final & Project 0.5 0.50
What values would you enter in the Risk Solver Platform RSP)task pane for the cells in this Excel spreadsheet implementation of this problem?
Objective Cell: Variables Cells: Constraints Cells:
12 Both Exams 0.65 0.70
13 Final & Project 0.5 0.50
What values would you enter in the Risk Solver Platform RSP)task pane for the cells in this Excel spreadsheet implementation of this problem?
Objective Cell: Variables Cells: Constraints Cells:
(Essay)
4.8/5  (34)
(34)
You have been given the following linear programming model and Excel spreadsheet to solve this problem.What cell references would you enter in the Risk Solver Platform RSP)task pane for the following?
Objective Cell:
Variables Cells:
Constraints Cells:
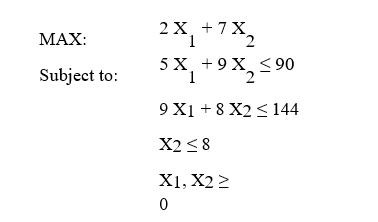 1 2 3 4 Number to make: OBJ. FN. VALUE 5 Unit profit: 1 9 2 6 7 Constraints: Used Available 8 1 9 10.5 12 6 9 2 1 0 5 10 3 0 1 6
1 2 3 4 Number to make: OBJ. FN. VALUE 5 Unit profit: 1 9 2 6 7 Constraints: Used Available 8 1 9 10.5 12 6 9 2 1 0 5 10 3 0 1 6
(Essay)
5.0/5  (37)
(37)
Exhibit 3.1
The following questions are based on this problem and accompanying Excel windows.
Jones Furniture Company produces beds and desks for college students.The production process requires carpentry and varnishing.Each bed requires 6 hours of carpentry and 4 hour of varnishing.Each desk requires 4 hours of carpentry and 8 hours of varnishing.There are 36 hours of carpentry time and 40 hours of varnishing time available.Beds generate $30 of profit and desks generate $40 of profit.Demand for desks is limited,so at most 8 will be produced.
Let X1 = Number of Beds to produce X2 = Number of Desks to produce
The LP model for the problem is
MAX: 30 X1 + 40 X2
Subject to: 6 X1 + 4 X2 ≤ 36 carpentry)
4 X1 + 8 X2 ≤ 40 varnishing)X2 ≤ 8 demand for desks)X1,X2 ≥ 0
1 Jones Furnit 2 ure 3 4 Number to make: Total Profit: 5 Unit profit: 30 40 6 7 Constraints: Use Available 8 Carpentry 6 4 36 9 Varnishing 4 8 40 10 Desk demand 1 8
-Refer to Exhibit 3.1.What formula should be entered in cell E5 in the accompanying Excel spreadsheet to compute total profit?
(Multiple Choice)
4.8/5  (29)
(29)
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
Week Trucking Limits Railway Limits Air Cargo Limits 1 45 60 15 2 50 55 10 3 55 45 5 Costs \ per 1000 tons) \ 20 \ 14 \ 40 0 0 0
Formulate an LP model for this logistics problem.
(Essay)
4.9/5  (41)
(41)
Exhibit 3.2
The following questions are based on this problem and accompanying Excel windows.
The Byte computer company produces two models of computers,Plain and Fancy.It wants to plan how many computers to produce next month to maximize profits.Producing these computers requires wiring,assembly and inspection time.Each computer produces a certain level of profits but faces only a limited demand.There are also a limited number of wiring,assembly and inspection hours available in each month.The data for this problem is summarized in the following table.
Maximum Assembly Inspection Computer Profit per demand for Wiring Hours Hours Hours Model Model \ ) product Required Required Required Plain 30 80 .4 .5 .2 Fancy 40 90 .5 .4 .3 hours avaible 50 50 22 Let X1 = Number of Plain computers to produce X2 = Number of Fancy computers to produce
MAX: 30 X1 + 40 X2
Subject to: .4 X1 + .5 X2 ≤ 50 wiring hours)
.5 X1 + .4 X2 ≤ 50 assembly hours)
.2 X1 + .2 X2 ≤ 22 inspection hours)X1 ≤ 80 Plain computers demand)X2 ≤ 90 Fancy computers demand)X1,X2 ≥ 0
A B C D E 1 Byte Computer Company 2 3 Plain Fancy 4 Number to make: Total Profit: 5 Unit profit: 30 40 6 7 Constraints: Used Available 8 Wiring 0.4 0.5 50 9 Assembly 0.5 0.4 50 10 Inspection 0.2 0.3 22 11 Plain Demand 1 80 12 Fancy Demand 1 90
-Refer to Exhibit 3.2.Which cells should be changing cells in this problem?
(Multiple Choice)
4.7/5  (35)
(35)
The "Objective Value of" option in the Analytic Solver Platform task pane may be used to
(Multiple Choice)
4.9/5  (41)
(41)
Exhibit 3.2
The following questions are based on this problem and accompanying Excel windows.
The Byte computer company produces two models of computers,Plain and Fancy.It wants to plan how many computers to produce next month to maximize profits.Producing these computers requires wiring,assembly and inspection time.Each computer produces a certain level of profits but faces only a limited demand.There are also a limited number of wiring,assembly and inspection hours available in each month.The data for this problem is summarized in the following table.
Maximum Assembly Inspection Computer Profit per demand for Wiring Hours Hours Hours Model Model \ ) product Required Required Required Plain 30 80 .4 .5 .2 Fancy 40 90 .5 .4 .3 hours avaible 50 50 22 Let X1 = Number of Plain computers to produce X2 = Number of Fancy computers to produce
MAX: 30 X1 + 40 X2
Subject to: .4 X1 + .5 X2 ≤ 50 wiring hours)
.5 X1 + .4 X2 ≤ 50 assembly hours)
.2 X1 + .2 X2 ≤ 22 inspection hours)X1 ≤ 80 Plain computers demand)X2 ≤ 90 Fancy computers demand)X1,X2 ≥ 0
A B C D E 1 Byte Computer Company 2 3 Plain Fancy 4 Number to make: Total Profit: 5 Unit profit: 30 40 6 7 Constraints: Used Available 8 Wiring 0.4 0.5 50 9 Assembly 0.5 0.4 50 10 Inspection 0.2 0.3 22 11 Plain Demand 1 80 12 Fancy Demand 1 90
-Refer to Exhibit 3.2.Which cells should be the constraint cells in this problem?
(Multiple Choice)
4.9/5  (38)
(38)
Showing 21 - 40 of 75
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)