Exam 6: Integer Linear Programming
Exam 1: Introduction to Modeling and Decision Analysis74 Questions
Exam 2: Introduction to Optimization and Linear Programming73 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet75 Questions
Exam 4: Sensitivity Analysis and the Simplex Method77 Questions
Exam 5: Network Modeling84 Questions
Exam 6: Integer Linear Programming88 Questions
Exam 7: Goal Programming and Multiple Objective Optimization65 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization69 Questions
Exam 9: Regression Analysis82 Questions
Exam 10: Data Mining102 Questions
Exam 11: Time Series Forecasting81 Questions
Exam 12: Introduction to Simulation Using Analytic Solver Platform70 Questions
Exam 13: Queuing Theory87 Questions
Exam 14: Decision Analysis116 Questions
Exam 15: Project Management Online65 Questions
Select questions type
A practical way of dealing with the complexity of IP problems is to:
(Multiple Choice)
4.8/5  (35)
(35)
A production company wants to ensure that if Product 1 is produced,production of Product 1 not exceed production of Product 2.Which of the following constraints enforce this condition?
(Multiple Choice)
4.9/5  (39)
(39)
A city wants to locate 2 new fire fighting ladder trucks to maximize the number of tall buildings which they can cover within a 3 minute response time.The city is divided into 4 zones.The fire chief wants to locate no more than one of the trucks in either Zone 1 or Zone 2.The number of tall buildings in each zone and the travel time between zones is listed below.
To zone No. tall buildings Fram zone 1 2 3 4 50 1 0 2 1 6 90 2 2 0 4 5 60 3 1 4 0 1 70 4 6 5 1 0
Based on this ILP formulation of the problem what values should go in cells B5:G24 of the following Excel spreadsheet?
Let Xi = 1 if truck located in zone i,0 otherwise
Zone Covers these zones With the many building 1 1,2,3 200 2 1,2 140 3 1,3,4 180 4 3,4 130
MAX: 200 X1 + 140 X2 + 180 X3 + 130 X4
Subject to: X1 + X2 + X3 + X4 = 2
X1 + X2 ? 1
Xi = 0,1
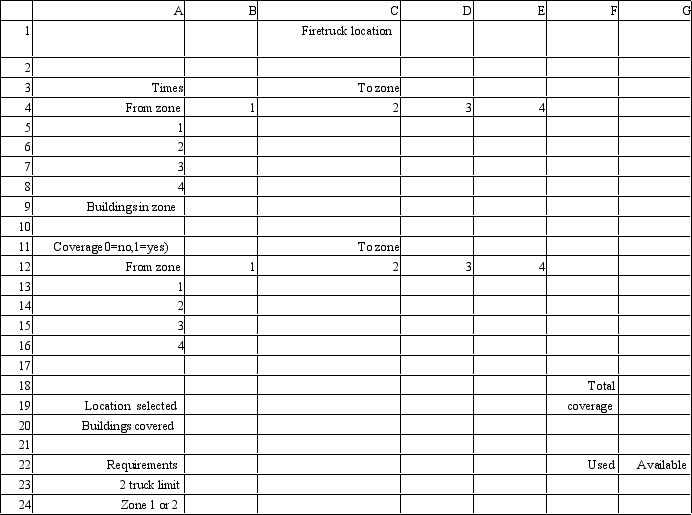
(Essay)
4.8/5  (36)
(36)
A vendor offers 5 different prices per unit depending on the quantity purchased.How many binary variables are needed to model this discounting scheme?
(Multiple Choice)
4.8/5  (31)
(31)
A cellular phone company wants to locate two new communications towers to cover 4 regions.The company wants to minimize the cost of installing the two towers.The regions that can be covered by each tower site are indicated by a 1 in the following table:
Tower Sites
Region 1 2 3 4 A 1 1 B 1 1 1 C 1 1 1 D 1 1 COST \ 000 s) 200 150 190 250
MIN: 200 X1 + 150 X2 + 190 X3 + 250 X4
Subject to: X2 + X4 ? 1
X1 + X3 + X4 ? 1 X1 + X2 + X3 ? 1 X1 + X4 ? 1
X1 + X2 + X3 + X4 = 2 Xi = 0,1
Based on this ILP formulation of the problem what formulas should go in cells F6:F14 of the following Excel spreadsheet?
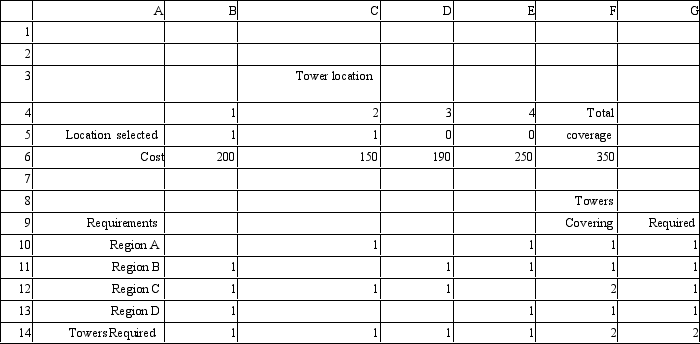
(Essay)
4.9/5  (37)
(37)
Exhibit 6.2
The following questions pertain to the problem,formulation,and spreadsheet implementation below.
A certain military deployment requires supplies delivered to four locations.These deliveries come from one of three ports.Logistics planners wish to deliver the supplies in an efficient manner,in this case by minimizing total ton-miles.The port-destination data,along with destination demand is provided in the following table.
Destination
Port D1 D2 D3 D4 A 75 88 103 56 105 76 101 85 43 80 95 82 Demand 500 600 450 700 The ports are supplied by one of two supply ships.These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations.Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies.These ships can only go to a single port and each port can only accommodate one ship.
Assume the costs for a ship to travel to a port are not part of the objective function.The following is the ILP formulation and a spreadsheet model for the problem.
Let Yij be 1 if ship i travels to port j,for i = S1,S2 and j = A,B,C
Xjk be the tons shipped from port j = A,B,C to Destination k = D1,D2,D3,D4
Minimize 75X11 + 88X12 + 103X13 + 56X14 + 105X21 + 76X22 + 101X23 + 85X24
+ 43X31 + 80X32 + 95X33 + 62X34
Subject to: Y11 + Y21 ? 1
Y12 + Y22 ? 1 Y13 + Y23 ? 1
Y11 + Y12 + Y13 = 1 Y21 + Y22 + Y23 = 1
X14 + X15 + X16 + X17 ? 1200Y11 + 1120Y21 X24 + X25 + X26 + X27 ? 1200Y12 + 1120Y22 X34 + X35 + X36 + X37 ? 1200Y13 + 1120Y23 X14 + X24 + X34 ? 500
X15 + X25 + X35 ? 600 X16 + X26 + X36 ? 450 X17 + X27 + X37 ? 700
Yij.Xjk ? 0
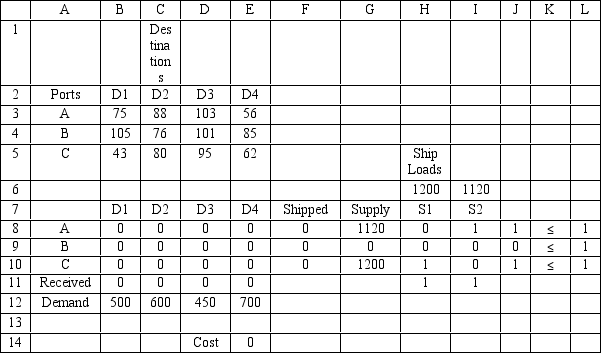 -Refer to Exhibit 6.2.What formula would go into cells B11:E11 and cells F8:F10?
-Refer to Exhibit 6.2.What formula would go into cells B11:E11 and cells F8:F10?
(Essay)
4.9/5  (41)
(41)
For maximization problems,the optimal objective function value to the LP relaxation provides what for the optimal objective function value of the ILP problem?
(Multiple Choice)
4.9/5  (42)
(42)
A company is developing its weekly production plan.The company produces two products,A and B,which are processed in two departments.Setting up each batch of A requires $60 of labor while setting up a batch of B costs $80.Each unit of A generates a profit of $17 while a unit of B earns a profit of $21.The company can sell all the units it produces.The data for the problem are summarized below.
Hours required by
Operation A B Hours Cutting 3 4 48 Welding 2 1 36
What is the appropriate formula to use in cell B15 of the following Excel implementation of the ILP model for this problem?
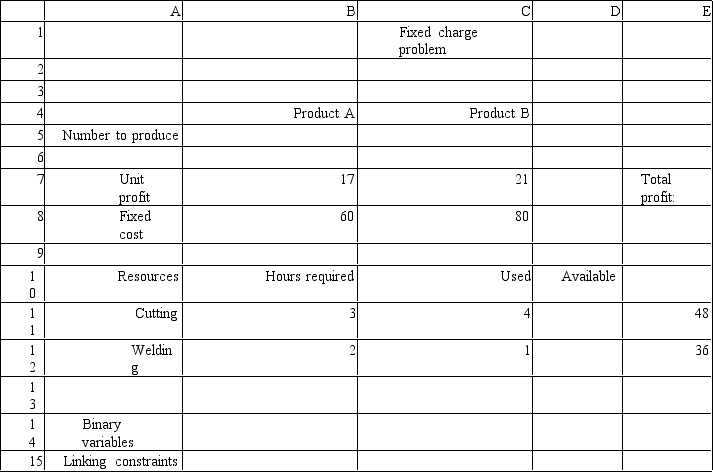
(Multiple Choice)
4.8/5  (26)
(26)
A small town wants to build some new recreational facilities.The proposed facilities include a swimming pool,recreation center,basketball court and baseball field.The town council wants to provide the facilities which will be used by the most people,but faces budget and land limitations.The town has $400,000 and 14 acres of land.The pool requires locker facilities which would be in the recreation center,so if the swimming pool is built the recreation center must also be built.Also the council has only enough flat land to build the basketball court or the baseball field.The daily usage and cost of the facilities in $1,000)are shown below.
Formulate the ILP for this problem.
Variable Facilty Usage Cost \1 ,000) Land Swimruine pool 400 100 2 Recreation center 500 200 3 Basketball court 300 150 4 Baseball field 200 100 5
(Essay)
4.9/5  (33)
(33)
An ILP problem has 5 binary decision variables.How many possible integer solutions are there to this problem?
(Multiple Choice)
4.8/5  (35)
(35)
What does the Analytic Solver Platform default integer tolerance factor of 0 accomplish?
(Multiple Choice)
4.9/5  (31)
(31)
The following ILP is being solved by the branch and bound method.You have been given the initial relaxed IP solution.Complete the entries for the 3 nodes and label the arcs when you branch on X2.
MAX: 50 X1 + 40 X2
Subject to: 2 X1 + 4 X2 ≤ 40
3 X1 + 2 X2 ≤ 30
X1,X2 ≥ 0 and integer
Initial solution X1 = 5.0
X2 = 7.5
Obj = 550 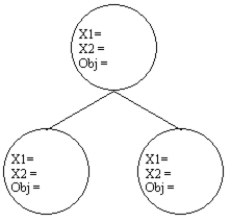
(Essay)
4.8/5  (38)
(38)
A company must invest in project 1 in order to invest in project 2.Which of the following constraints ensures that project 1 will be chosen if project 2 is invested in?
(Multiple Choice)
4.9/5  (35)
(35)
How are binary variables specified in the Analytic Solver Platform ASP)?
(Multiple Choice)
4.7/5  (28)
(28)
A sub-problem in a B & B is solved and found infeasible.Should the B & B algorithm continue further analysis on this candidate problem?
(Multiple Choice)
4.8/5  (33)
(33)
The optimal relaxed solution for an ILP has X1 = 3.6 and X2 = 2.9.If we branch on X1,what constraints must be added to the two resulting LP problems?
(Multiple Choice)
4.8/5  (25)
(25)
Showing 41 - 60 of 88
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)