Exam 6: Integer Linear Programming
Exam 1: Introduction to Modeling and Decision Analysis74 Questions
Exam 2: Introduction to Optimization and Linear Programming73 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet75 Questions
Exam 4: Sensitivity Analysis and the Simplex Method77 Questions
Exam 5: Network Modeling84 Questions
Exam 6: Integer Linear Programming88 Questions
Exam 7: Goal Programming and Multiple Objective Optimization65 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization69 Questions
Exam 9: Regression Analysis82 Questions
Exam 10: Data Mining102 Questions
Exam 11: Time Series Forecasting81 Questions
Exam 12: Introduction to Simulation Using Analytic Solver Platform70 Questions
Exam 13: Queuing Theory87 Questions
Exam 14: Decision Analysis116 Questions
Exam 15: Project Management Online65 Questions
Select questions type
A company produces three products which must be painted,assembled,and inspected.The machinery must be cleaned and adjusted before each batch is produced.They want to maximize their profits for the amount of operating time they have.The unit profit and setup cost per batch are:
Product Profit per unit Setup cost per batch 1 9 500 2 10 600 3 12 650
The operation time per unit and total operating hours available are:
Operating Time per Unit Operation Product 1 Product 2 Product 3 Operating Hours Available Paint 1 2 2 400 Assemble 2 3 2 600 Inspection 2 4 3 540
Based on this ILP formulation of the problem and the optimal solution X1,X2,X3)= 270,0,0),what values should appear in the shaded cells in the following Excel spreadsheet?
Xi = amount of product i produced
Yi = 1 if product i produced,0 otherwise
MAX: 9 X1 + 10 X2 + 12 X3 ? 500 Y1 ? 600 Y2 ? 650 Y3
Subject to: 1 X1 + 2 X2 + 2 X3 ? 400
2 X1 + 3 X2 + 2 X3 ? 600
2 X1 + 4 X2 + 3 X3 ? 540 X1 ? M1 Y1 OR 270 Y1 X2 ? M2 Y2 OR 135 Y2 X3 ? M3 Y3 OR 180 Y3 Yi = 0,1
Xi ? 0 and integer
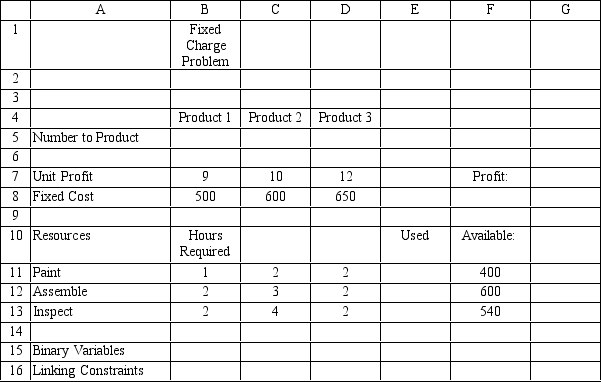
(Essay)
4.9/5  (31)
(31)
A company is developing its weekly production plan.The company produces two products,A and B,which are processed in two departments.Setting up each batch of A requires $60 of labor while setting up a batch of B costs $80.Each unit of A generates a profit of $17 while a unit of B earns a profit of $21.The company can sell all the units it produces.The data for the problem are summarized below.
Hours required by
Operation A B Hours Cutting 3 4 48 Welding 2 1 36
What is the appropriate formula to use in cell E8 of the following Excel implementation of the ILP model for this problem?
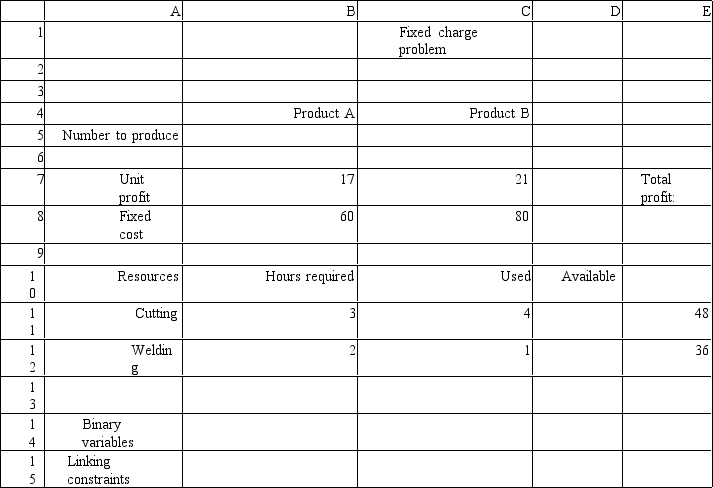
(Multiple Choice)
4.9/5  (29)
(29)
How is the integer tolerance factor set in the Analytic Solver Platform ASP)?
(Multiple Choice)
4.9/5  (39)
(39)
If a company selects either of Project 1 or Project 2 or both),then either Project 3 or Project 4 or both)must also be selected.Which of the following constraints enforce this condition?
(Multiple Choice)
4.9/5  (39)
(39)
Project 6.2 ? Dayton Electronics Manufacturing Inc.DEMI)
The Dayton Electronic Manufacturing,Inc DEMI)company manufactures two styles of remote keyless entry systems the X30 and the X40)that various auto dealers supply to customers when a new or used)automobile is purchased.DEMI currently operates four production facilities located in Springfield OH,Hartford,New Orleans,and Orlando.The manufactured items are shipped from the plants to regional distribution centers located in Trenton,Chicago and Seattle.It is from these regional locations that the product is distributed nationwide.
As more automobile manufactures include keyless entry as a standard option,and DEMI finds itself locked out of the manufacturer market,demand for DEMI's products have decreased.As a result,management is contemplating closing one or more of its production facilities.Distribution facilities are not currently being considered for closing.
Each production facility carries a fixed operating cost and a variable cost associated with building each of the products.Data has been compiled on production costs,resource availability,and resource usage at each of the production plants.That information is summarized in the table below.
Plant Fixed Cost Per Month \ 1000 ) Production Cost per 100 ) X 30-40 Production Time /100 ) 30-40 Available Hours per Month Springfield 53 11001300 66 720 Hartford 38 11001250 78 780 New Orleans 25 10001000 55 530 Orlando 28 12001500 59 680
The entry systems are sold nationwide at the same prices: $24 for the X30 and $30 for the X40.
Current monthly demand projections at each distribution center for both products are given in the following table.
Demand Trenton Chicago Seattle X30 2200 3100 4000 X40 4500 5800 6000
The transportation costs between each plant and each distribution center,which are the same for either product,are shown in the following table:
From Trenton Chicago Seattle Springfield \ 200 \ 270 \ 450 Hartford \ 100 \ 200 \ 700 New Orleans \ 250 \ 240 \ 300 Orlando \ 180 \ 220 \ 350
• Determine which of the plants to close and which to keep open.
• Determine the number of X30 and X40 to be produced at each plant.
• Determine a shipping pattern from the plants to the distribution centers.
• Maximize the net total monthly profit.If any plants were closed,what was the impact of the closing on profits?
• Do not exceed the production capacities at any plant.
Formulate DEMI's problem as a fixed charge,integer program.Implement your model in Excel and solve the model to answer DEMI's questions.
(Essay)
4.8/5  (38)
(38)
A company wants to select 1 project from a set of 4 possible projects.Which of the following constraints ensures that only 1 will be selected?
(Multiple Choice)
4.8/5  (41)
(41)
Showing 81 - 88 of 88
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)