Exam 14: Random Variables

Hugh buys $8000 worth of stock in an electronics company which he hopes to sell afterward at a profit.The company is developing a new laptop computer and a new desktop computer.If it releases both computers before its competitor,the value of Hugh's stock will jump to $22,000.If it releases one of the computers before its competitor,the value of Hugh's stock will jump to $16,000.If it fails to release either computer before its competitor,Hugh's stock will be worth only $5000.Hugh believes that there is a 70% chance that the company will release the laptop before its competitor and a 60% chance that the company will release the desktop before its competitor.Find Hugh's expected profit.Assume that the development of the laptop and the development of the desktop are independent events.

A tennis player makes a successful first serve 60% of the time.If she serves 25 times,what is the mean of the number of good first serves? Assume that each serve is independent of the others.

People with O-negative blood are called "universal donors" because O-negative blood can be given to anyone else regardless of the recipient's blood type.About 6% of people have type O-negative blood. A clinic is running a blood drive.If at least 220 O-negative donors give blood,the clinic will have sufficient O-negative blood for the coming month.If 4000 donors come to the blood drive,what is the probability that the clinic will not have sufficient O-negative donors?

At a furniture factory,tables must be assembled,finished,and packaged before they can be shipped to stores.Based on past experience,the manager finds that the means and standard deviations (in minutes)of the times for each phase are as shown in the table: Phase Mean SD Assembly 25.4 2.6 Finishing 35.5 3.6 Packaging 14.6 1.8 What are the mean and standard deviation of the total time to prepare a table for shipping? Assume that the times for each phase are independent.

An insurance company estimates that it should make an annual profit of $150 on each homeowner's policy written,with a standard deviation of $6700.If it writes 12,469 of these policies,what is the probability that the company will be profitable? Assume that policies are independent of each other and that the company's total profit follows a Normal model.

Consider a random variable,X,with Uniform density over the range 0 to 1. 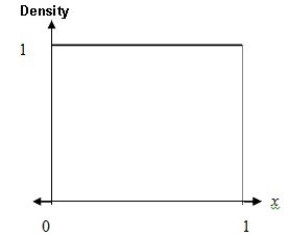What is P(0.2 < X < 0.5 or 0.4 < X < 0.6)?

Miguel buys a large bottle and a small bottle of juice.The amount of juice that the manufacturer puts in the large bottle is a random variable with a mean of 1018 ml and a standard deviation of 9 ml.The amount of juice that the manufacturer puts in the small bottle is a random variable with a mean of 506 ml and a standard deviation of 3 ml.Let the random variable T represent the total amount of juice in the two bottles.Suppose that you use a Normal model to determine the probability that the total amount of juice,T,in the two bottles is more than 1543.0 ml.Which of the following assumptions are needed to find the probability in this way? A: The amount of juice in the large bottle is independent of the amount of juice in the small bottle. B: The amount of juice in each bottle follows a Normal model. C: The amount of juice in the large bottle is greater than the amount of juice in the small bottle.

Your school's soccer team plays two games against another soccer team.The probability that your team wins the first game is 0.6.If your team wins the first game,the probability that they also win the second game is 0.7.If your team loses the first game,the probability that they win the second game is 0.5.Let the random variable X be the number of games won by your team.Find the probability model for X.

Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable X - Y.Round to two decimal places if necessary. Mean SD 220 16 260 12

You roll a die 7 times and need to get at least three 2's to win the game.

The probability that a car will have a flat tire while driving through a certain tunnel is 0.00005.Use the Poisson approximation to the binomial distribution to find the probability that among 14,000 cars passing through this tunnel,exactly two will have a flat tire.

Consider a game that consists of dealing out a hand of two random cards from a deck of four cards.The deck contains the Ace of Spades (As),the Ace of Hearts (Ah),the King of Spades (Ks)and the 9 of Hearts (9h).Aces count as 1 or 11.Kings count as 10.You are interested in the total count of the two cards,with a maximum count of 21 (that is,AsAh = 12).Let X be the sum of the two cards.Find the expected value of X.

A teacher grading statistics homework finds that none of the students has made more than three errors.14% have made three errors,25% have made two errors,and 39% have made one error.Find the standard deviation of the number of errors in students' statistics homework.

How likely is it that in a group of 400 people,the majority have blue eyes,given that 22% of the population have blue eyes? Assume that the people are unrelated to each other.

You pick a card from a deck.If you get a club,you win $80.If not,you get to draw again (after replacing the first card).If you get a club the second time,you win $30.If not,you lose.Find the standard deviation of the amount you will win.

Janet is planning to rent a booth at a festival for a day to sell clothes that she has made.She sells jackets for $\$ 80$ and skirts for $\$ 50$ Her past experiences suggests that sales of jackets will have a mean of 6.5 with a standard deviation of 1.4,and sales of skirts will have a mean of 12.6 with a standard deviation of 2.7.The cost of renting the booth for the day is $\$ 180$ Let the random variable J represent the number of jackets that Janet sells and the random variable S represent the number of skirts that Janet sells.Express Janet's net income,I,in terms of J and S.

Find the probability of at least 2 girls in 10 births.Assume that male and female births are equally likely and that the births are independent events.

A basketball player has made 70% of his foul shots during the season.If he shoots 6 foul shots in tonight's game,what is the probability that he makes none of the shots?

You roll a fair die.If you get a number greater than 4,you win $70.If not,you get to roll again.If you get a number greater than 4 the second time,you win $30.Otherwise you win nothing. Create a probability model for the amount you win at this game.

Consider a random variable,X,with Uniform density over the range 0 to 1. 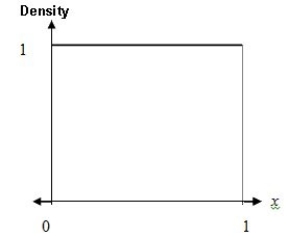What is P(0.2 < X < 0.5 and 0.4 < X < 0.6)?