Exam 14: Random Variables

Janet is planning to rent a booth at a festival for a day to sell clothes that she has made.She sells jackets for $175 and skirts for $130.Her past experiences suggests that the total number of jackets sold will have a mean of 7.0 with a standard deviation of 1.7,and the total number of skirts sold will have a mean of 11.7 with a standard deviation of 2.6.The cost of renting the booth for the day is $200.What are the mean and standard deviation of her net income? [Hint: you should first define random variables and use them to express her net income.]

In one city,police estimate that 79% of drivers wear their seat belts.They set up a safety roadblock and they stop drivers to check for seat belt use.If 150 drivers are stopped,is it appropriate to use a Normal model to approximate the distribution of the number whose seat belt is not buckled?

A tennis player makes a successful first serve 59% of the time.If she serves 29 times,what is the standard deviation of the number of good first serves? Assume that each serve is independent of the others.

Miguel buys a large bottle and a small bottle of juice.The amount of juice that the manufacturer puts in the large bottle is a random variable with a mean of 1018 ml and a standard deviation of 9 ml.The amount of juice that the manufacturer puts in the small bottle is a random variable with a mean of 506 ml and a standard deviation of 3 ml.Find the mean and standard deviation of the total amount of juice in the two bottles.

If Judy,who forgot to study for the test,guesses on all questions,what is the probability that she will answer none of the questions correctly?

The amount of cereal that a manufacturer puts in its boxes of cereal is a random variable with a mean of 1020 g and a standard deviation of 10 g.The amount of cereal that Tyler eats for breakfast is a random variable with a mean of 65 g and a standard deviation of 6 g.The amount of cereal that Tyler's wife,Suzanne,eats for breakfast is a random variable with a mean of 53 g and a standard deviation of 2 g.If Tyler and Suzanne open a new packet of cereal one Monday morning,find the mean and standard deviation of the amount of cereal remaining in the packet after one breakfast.Assume that the amount that Tyler eats is independent of the amount Suzanne eats.

20 40 60 (=) 0.2 0.3 0.5

x 20 40 60 P(X=x) 0.25 0.30 0.45

An archer is able to hit the bull's eye 74% of the time.If she shoots 130 arrows in a competition,is it appropriate to use a Normal model to approximate the distribution of the number of bull's-eyes? Assume that shots are independent of each other.

The number of lightning strikes in a year at the top of a particular mountain has a Poisson distribution with a mean of 2.8.Find the probability that in a randomly selected year,the number of lightning strikes is 2.

You roll a pair of fair dice.If you get a sum greater than 10 you win $50.If you get a double you win $40.If you get a double and a sum greater than 10 you win $90.Otherwise you win nothing. Create a probability model for the amount you win at this game.

Suppose a computer chip manufacturer rejects 15% of the chips produced because they fail presale testing.If you test 3 chips,what is the probability that not all of the chips fail?

Police estimate that 25% of drivers drive without their seat belts.If they stop 4 drivers at random,find the probability that all of them are wearing their seat belts.

The amount of money that Jon can save after working for a summer is a random variable S with a mean of $1500 and a standard deviation of $100.After saving this money Jon plans to go on a trip to India.He will change his money into Rupees at an exchange rate of 43 Rupees to one Dollar.This money he will bring to India.When he arrives in India he will buy a used motorbike.The price in India of a motorbike of the type he wants is a random variable B with a mean of 17,500 Rupees and a standard deviation of 600 Rupees.The amount of money Jon will have left (in Rupees)after changing his savings into Rupees and buying a motorbike in India is a random variable P which can be expressed in terms of S and B as $P = 43 S - B$ Find the mean and standard deviation of P in Rupees.Assume that Jon's savings and the price of the bike are independent.

If Judy,who forgot to study for the test,guesses on all questions,what is the probability that she will answer no more than 3 questions correctly?

A carnival game offers a(n)$80 cash prize for anyone who can break a balloon by throwing a dart at it.It costs $5 to play and you're willing to spend up to $20 trying to win.You estimate that you have a(n)10% chance of hitting the balloon on any throw. Create a probability model for the number of darts you will throw.Assume that throws are independent of each other.Round to four decimal places if necessary.

You pick a card from a deck.If you get a face card,you win $15.If you get an ace,you win $20 plus an extra $40 for the ace of hearts.For any other card you win nothing.Find the standard deviation of the amount you will win.

Consider a random variable,X,with Uniform density over the range 0 to 1. 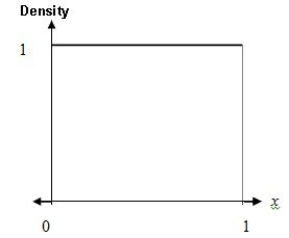What is P(0.2 < X < 0.7)?

An archer is able to hit the bull's eye 77% of the time.If she shoots 6 arrows,what is the standard deviation of the number of bull's-eyes that she gets? Assume the shots are independent of each other.

An archer is able to hit the bull's eye 48% of the time.If she shoots 8 arrows,how many bull's-eyes do you expect her to get? Assume the shots are independent of each other.