Exam 14: Random Variables

A tennis player makes a successful first serve 65% of the time.Assume that each serve is independent of the others.If she serves 5 times,what is the probability that she makes none of her first serves?

A tennis player makes a successful first serve 65% of the time.Assume that each serve is independent of the others.If she serves 5 times,what is the probability that she makes all of her first serves?

A carnival game offers a(n)$80 cash prize for anyone who can break a balloon by throwing a dart at it.It costs $5 to play and you're willing to spend up to $20 trying to win.You estimate that you have a(n)12% chance of hitting the balloon on any throw. Create a probability model for the amount you will win.Assume that throws are independent of each other.Round to four decimal places if necessary.

Consider a random variable,X,with Uniform density over the range 0 to 3.What is P(1.2 < X < 1.8)?

A company bids on two contracts.It anticipates a profit of $70,000 if it gets the larger contract and a profit of $40,000 if it gets the smaller contract.It estimates that there's a 30% chance of winning the larger contract and a 50% chance of winning the smaller contract.Find the company's expected profit.Assume that the contracts will be awarded independently.

Sue Anne owns a medium-sized business.The probability model below describes the number of employees that may call in sick on any given day. Number of Employees Sick 0 1 2 3 4 (=) 0.1 0.4 0.3 0.15 0.05 What is the expected value of the number of employees calling in sick each day?

We deal 6 cards from a deck and get 3 hearts.How likely is this?

The amount of time it takes to serve each customer in a bank is a random variable with a mean of 3.7 minutes and a standard deviation of 2.1 minutes.When you arrive at the bank there are three customers in front of you.The mean of your wait time is $3 \times 3.7 = 11.1$ minutes.The standard deviation of your wait time is $\sqrt { 2.1 ^ { 2 } + 2.1 ^ { 2 } + 2.1 ^ { 2 } } \approx 3.64$ minutes.What assumptions (if any)underlie the calculation of the mean? of the standard deviation?

A police department reports that the probabilities that 0,1,2,and 3 burglaries will be reported in a given day are 0.52,0.42,0.05,and 0.01,respectively.Find the standard deviation of the number of burglaries in a day.

A laboratory worker finds that 1.6% of his blood samples test positive for the HIV virus.In a random sample of 140 blood tests,what is the mean number that test positive for the HIV virus?

The rate of defects among CD players of a certain brand is 1.1%.Use the Poisson approximation to the binomial distribution to find the probability that among 270 such CD players received by a store,there is at most one defective.

Consider a random variable,X,with Uniform density over the range 0 to 1. 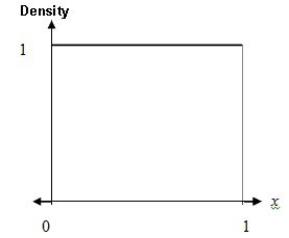Given that X is at least 0.4,find the probability that X is less than 0.6.

The amount of money that Jon can save after working for a summer is a random variable S with a mean of $1700 and a standard deviation of $100.After saving this money Jon plans to go on a trip to India.He will change his money into Rupees at an exchange rate of 43 Rupees to one Dollar.This money he will bring to India.When he arrives in India he will buy a used motorbike.The price in India of a motorbike of the type he wants is a random variable B with a mean of 18,500 Rupees and a standard deviation of 500 Rupees.The amount of money Jon will have left (in Rupees)after changing his savings into Rupees and buying a motorbike in India is a random variable P.Write an expression for P in terms of S and B.

Suppose that 11% of people are left handed.If 26 people are selected at random,what is the mean number of right-handers in the group?

If X and Y are independent random variables then the standard deviation of the random variable $X - Y$ is given by which of the following expressions?