Exam 7: Introduction to Probability
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
Suppose a fair coin is tossed 6 times. What is the probability of flipping exactly 2 heads?
(Multiple Choice)
4.8/5  (31)
(31)
In a 10-question matching test with 10 possible answers to match and no answer used more than once, what is the probability of guessing and getting every answer correct?
(Multiple Choice)
4.8/5  (28)
(28)
How many three-digit numbers can be formed from the digits 1, 3, 5, 7, 8, and 9 if each digit can be used at most once in each number?
(Multiple Choice)
4.8/5  (34)
(34)
An urn contains 4 red, 7 white, and 9 black balls. One ball is drawn from the urn, it is replaced, and a second ball is drawn. Construct a probability tree to determine the probability that both balls are white W.
(Multiple Choice)
4.7/5  (36)
(36)
A man owns an Audi, a Ford, and a VW. He drives every day and never drives the same car two days in a row. These are the probabilities that he drives each of the other cars the next day:
Pr(Ford after Audi) = 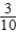 Pr(VW after Audi) =
Pr(VW after Audi) = 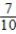 Pr(Audi after Ford) =
Pr(Audi after Ford) = 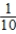 Pr(VW after Ford) =
Pr(VW after Ford) = 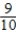 Pr(Audi after VW) =
Pr(Audi after VW) =  Pr(Ford after VW) =
Pr(Ford after VW) = 
What is the steady-state vector for this problem?
What is the steady-state vector for this problem?
(Multiple Choice)
4.9/5  (38)
(38)
An urn contains three red R balls numbered 1, 2 and 3, four white W balls numbered 4, 5, 6 and 7, and three black B balls numbered 8, 9 and 10 A ball is drawn from the urn. What is the probability that it is red and odd-numbered O?
(Multiple Choice)
4.8/5  (22)
(22)
A survey questioned 1000 people regarding raising the legal drinking age from 18 to 21. Of the 560 people who favored raising the legal drinking age, 390 were female. Of the 440 opposition responses, 120 were female. If a person selected at random from this group is a man, what is the probability that the person favors raising the drinking age?
(Multiple Choice)
4.7/5  (28)
(28)
An automatic teller machine requires that each customer enter a three-digit personal identification number (PIN) when he or she inserts a bank card. If a person finds a bank card and guesses at a PIN to use the card fraudulently, what is the probability that the person will succeed in one attempt?
(Multiple Choice)
4.8/5  (36)
(36)
One ball is drawn at random from a bag containing 17 red R balls and 5 white W balls. What is the probability that the ball is green G?
(Multiple Choice)
4.8/5  (38)
(38)
A senator asks his constituents to rank seven issues in order of importance. What is the probability that one reply chosen at random will rank the issues in alphabetical order?
(Multiple Choice)
4.9/5  (37)
(37)
A department store manager wants to display 4 brands of a product along one shelf of an aisle. In how many ways can he arrange the brands?
(Multiple Choice)
4.8/5  (26)
(26)
The following table gives the results of a 2005 survey of 1000 people regarding the funding of universal health care by employers (employer mandate).
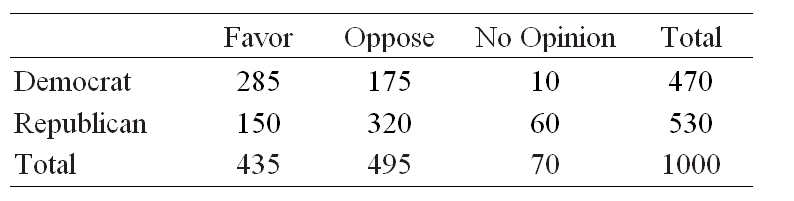 What is the probability that a person selected at random from this group will favor universal health care F with an employer mandate, given that the person is a Democrat D?
What is the probability that a person selected at random from this group will favor universal health care F with an employer mandate, given that the person is a Democrat D?
(Multiple Choice)
4.8/5  (34)
(34)
A bag contains 7 white, 9 black, and 10 green balls. What is the probability that a ball drawn at random from the bag is white W or green G?
(Multiple Choice)
4.9/5  (36)
(36)
A computer store offers used computers free to local middle schools. Of the 55 machines available, 15 have defective memories, 12 have defective keys, and the remainder have no defects. If a teacher picks one at random, what is the probability that she will select a defective computer?
(Multiple Choice)
4.9/5  (38)
(38)
For species that reproduce sexually, characteristics are determined by a gene from each parent. Suppose that for a certain trait there are two possible genes available from each parent: a dominant gene D and a recessive gene r. Then the different gene combinations (called genotypes) for the offspring are DD, Dr, rD, and rr, where Dr and rD produce the same trait. Suppose further that these genotypes are the states of a Markov chain with the transition matrix given below. If the initial occurrence of those genotypes in the population is 0.1 for DD, 0.2 for Dr, and 0.7 for rr, find the distribution (probability) of each type of the second generation of offspring. Round all numerical values in your answer to two decimal places. 
(Multiple Choice)
4.8/5  (34)
(34)
One ball is drawn at random from a bag containing 13 red R balls and 8 white W balls. What is the probability that the ball is red?
(Multiple Choice)
4.9/5  (28)
(28)
The following table gives the percent of employees of the Ace Company in each of three salary brackets, categorized by the sex of the employees. An employee is selected at random. What is the probability that the person selected makes at least $50,000?
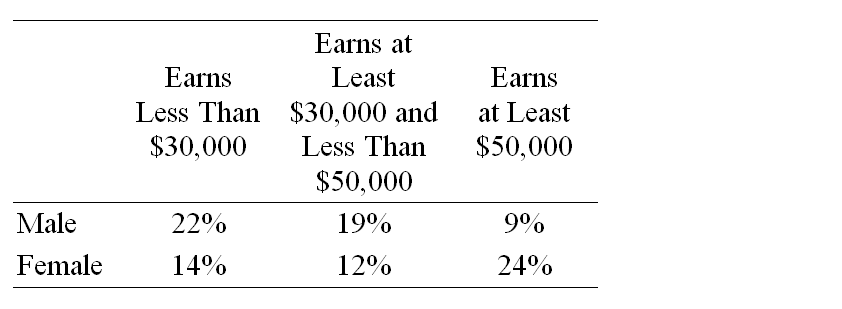
(Multiple Choice)
5.0/5  (46)
(46)
A bag contains 6 red balls numbered 1-6 and 14 white balls numbered 7-20. If a ball is drawn, what is the probability that the ball is red R or even-numbered E?
(Multiple Choice)
5.0/5  (30)
(30)
Suppose that an employer plans to hire four people from a group of eleven equally qualified people, of whom three are minority candidates. If the employer does not know which candidates are minority candidates, and if she selects her employees at random, what is the probability that no minority candidates are hired? Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (39)
(39)
In a sales promotion, a clothing store gives its customers a chance to draw a ticket from a box that contains a discount on their next purchase. The box contains 9000 tickets giving a 10% discount, 900 giving a 30% discount, 450 giving a 50% discount, and 4 giving a 100% discount. What is the probability that a given customer will randomly draw a ticket giving a 50% discount?
(Multiple Choice)
4.9/5  (41)
(41)
Showing 21 - 40 of 180
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)