Exam 7: Introduction to Probability

The 2003 Toyota Matrix was first made available with 5 different engines and with 6 levels of trim, plus either front-wheel or all-wheel drive. How many different Toyota Matrix cars models were available for purchase? ​

Three balls are drawn, without replacement, from a bag containing 9 red balls and 7 white balls. Construct a probability tree to determine the probability that two white W balls and one red R ball are drawn in any order. ​

In a certain city, the Democratic, Republican, and Consumer parties always nominate candidates for mayor. The probability of winning in any election depends on the party in power and is given by the following transition matrix. ​ ​ Using the given transition matrix and assuming the initial-probability vector is 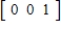, find the probability vector for the fourth stage of the Markov chain. (This initial-probability vector indicates that a Consumer is certain to win the initial election.) ​

A box of 11 transistors has 7 defective ones. If 2 transistors are drawn from the box together, what is the probability that both transistors are defective? Round your answer to two decimal places. ​

A bag contains 5 coins, of which 4 are fair; the remaining coin has a head on both sides. If a coin is selected at random from the bag and tossed three times, construct a probability tree to determine the probability that heads will occur at least twice. ​

Suppose a country has 1,000,000 registered voters, 370,000 of whom are Democrats and 430,000 of whom are Republicans. If a registered voter is chosen at random, what is the probability that he or she is neither a Democrat nor a Republican? ​

An unprepared student must take a 7-question, multiple-choice test that has 5 possible answers per question. If the student can eliminate 2 of the possible answers on the first 4 questions, and if she guesses on every question, what is the probability that she will answer every question correctly? ​

An urn contains two red R balls numbered 1 and 2, five white W balls numbered 3, 4, 5, 6 and 7, and three black B balls numbered 8, 9 and 10. A ball is drawn from the urn. What is the probability that it is red or odd-numbered O? ​

Suppose a box contains 7 defective transistors and 16 good transistors. If 2 transistors are drawn from the box without replacement, what is the probability that the first transistor is defective D and the second one is good G? ​

Suppose a box contains 2 defective transistors and 12 good transistors. If 2 transistors are drawn from the box without replacement, what is the probability that the first transistor is good G and the second transistor is defective D? ​

Suppose that an employer plans to hire six people from a group of nine equally qualified people, of whom two are minority candidates. If the employer does not know which candidates are minority candidates, and if she selects her employees at random, what is the probability that all two minority candidates are hired? Round your answer to six decimal places. ​

How many four-digit numbers can be formed from the digits 1, 3, 5, 7, 8, and 9 if the numbers mast be even and digits are not repeated? (Hint: Begin with the digit where there is a restriction on the choices.) ​

A dry cleaning firm has 6 employees: 4 women and 2 men. 2 of the women and 1 of the men are 42 years old or older. The remainder are over 20 years of age and under 42. If a person is chosen at random from this firm, what is the probability that the person is under 42 years of age? ​

A bag contains 11 red balls numbered 1-11 and 12 white balls numbered 12-23. If a ball is drawn, what is the probability that the ball is red R and even-numbered E? ​

A senator asks his constituents to rank six issues in order of importance. How many rankings are possible? ​

In how many ways can a committee consisting of 3 men and 7 women be selected from a group consisting of 20 men and 17 women? ​

Suppose a box contains 6 defective transistors and 13 good transistors. If 2 transistors are drawn from the box without replacement, what is the probability that one of the transistors drawn is good G and one of them is defective D? ​

Compute ​

Five percent of the population of the United States has type AB blood. What is the probability, rounded to two decimal places, that a U.S. resident chosen at random will have type AB blood? ​

A box contains 3 red balls, 5 white balls, and 3 black balls. Two balls are drawn at random from the box with replacement of the first before the second is drawn.What is the probability of getting a red R ball on the first draw and a white W ball on the second? ​