Exam 7: Introduction to Probability
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
A bag contains 3 nickels, 5 dimes, and 4 quarters. If you draw 3 coins at random from the bag, without replacement, what is the probability that you will get a nickel N, a quarter Q, and a nickel N, in that order?
(Multiple Choice)
4.7/5  (29)
(29)
The following table gives the numbers of AIDS deaths in a single year for people over age 13 in various categories. Use the table to find the probability, rounded to four decimal places, that a person who died of AIDS in this year was Hispanic. 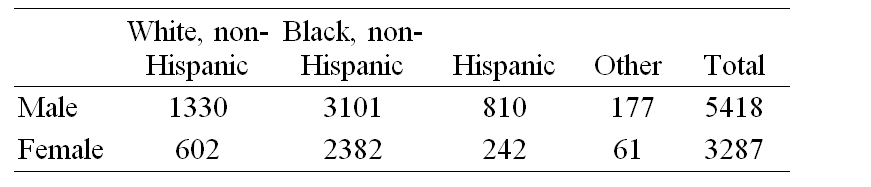
(Multiple Choice)
4.9/5  (28)
(28)
A box of 26 transistors has 3 defective ones. If 2 transistors are drawn from the box together, what is the probability that neither transistor is defective? Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
A card is drawn from an ordinary deck of 52 playing cards. Given that it is a jack(J), queen(Q) or king(K), what is the probability that a jack was drawn?
(Multiple Choice)
4.8/5  (30)
(30)
If a state wants each of its license plates to contain 6 different digits, how many different license plates can it make if any of the digits 0 through 9 can appear in any of the 6 positions?
(Multiple Choice)
4.9/5  (45)
(45)
The probability that a wife W watches a certain television show is 0.31, that her husband H watches it is 0.21, and that both watch the show is 0.05. What is the probability, to two decimal places, that either the husband or the wife watches this show?
(Multiple Choice)
4.8/5  (37)
(37)
The probability that daughters of a mother who attends church regularly will also attend church regularly is 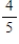 , whereas the probability that daughters of a mother who does not attend regularly will attend regularly is
, whereas the probability that daughters of a mother who does not attend regularly will attend regularly is 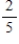 . What is the steady-state vector for this information?
. What is the steady-state vector for this information?
(Multiple Choice)
4.8/5  (31)
(31)
Lactose intolerance affects about 10% of non-Hispanic white Americans, 50% of Hispanic Americans, and 70% of African, Asian, and Native Americans. Seventy-four percent of U.S. residents are non-Hispanic whites, 10% of them are Hispanic, and 11% are African, Asian, or Native American. If a person is selected from this group of people, what is the probability, to four decimal places, that the person will be lactose intolerant?
(Multiple Choice)
4.7/5  (41)
(41)
The following table gives the percent of employees of the Ace Company in each of three salary brackets, categorized by the sex of the employees. An employee is selected at random. What is the probability that the person is male or makes less than $30,000?
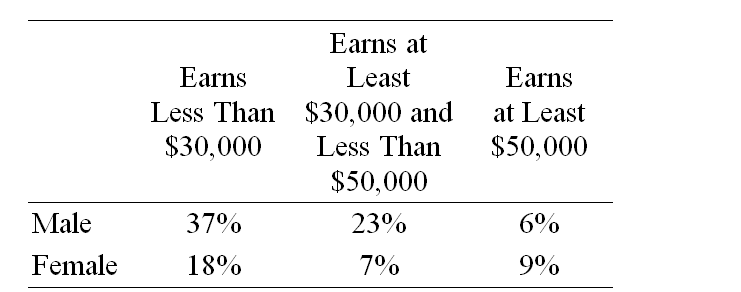
(Multiple Choice)
4.8/5  (27)
(27)
From a deck of 52 playing cards, two cards are drawn, one after the other without replacement. What is the probability that the first will be a king and the second will be a jack of the same suit?
(Multiple Choice)
4.8/5  (34)
(34)
In one state there is a lottery game called Pick 4. The state chooses 12 numbers from 46 numbers, and each player chooses 4 numbers from the same 46 numbers. If all 4 of a player's numbers are among the 12 numbers that the state picked, then that player is a "big winner." Find the probability of being a big winner. Round your answer to four decimal places.
(Multiple Choice)
5.0/5  (34)
(34)
A bag contains 11 red balls and 13 white balls. Two balls are drawn without replacement. What is the probability that the second ball is white W, given that the first ball is red R?
(Multiple Choice)
4.9/5  (30)
(30)
A mathematics class consists of 17 engineering majors E, 13 science majors S, and 9 liberal arts majors LA. Twelve of the engineering students, 3 of the science majors, and 3 of the liberal arts majors are female. What is the probability that a student selected at random is an engineering major or is a female F?
(Multiple Choice)
4.8/5  (41)
(41)
Find the steady-state vector associated with the transition matrix  . Round all numerical values in your answer to two decimal places.
. Round all numerical values in your answer to two decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
Suppose that an employer plans to hire eight people from a group of fourteen equally qualified people, of whom four are minority candidates. If the employer does not know which candidates are minority candidates, and if she selects her employees at random, what is the probability that exactly one minority candidate is hired? Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (41)
(41)
A mathematics class consists of 9 engineering majors E, 14 science majors S, and 8 liberal arts majors LA. What is the probability that a student selected at random will be a science or liberal arts major?
(Multiple Choice)
4.8/5  (36)
(36)
A bag contains 5 white balls and 5 red balls. Construct a probability tree to determine the probability that if 2 balls are drawn,with replacement, one ball is red R and one is white W.
(Multiple Choice)
4.9/5  (37)
(37)
A small town has 5000 adult males and 7000 adult females. A sociologist conducted a survey and found that 40% of the males and 30% of the females drink heavily. An adult is selected at random from the town. What is the probability, rounded to four decimal places, that the person is male M or drinks heavily DH?
(Multiple Choice)
4.9/5  (34)
(34)
On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997). Suppose the probability of an amateur golfer getting a hole-in-one is 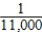 . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one?
. If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one?
(Multiple Choice)
4.8/5  (24)
(24)
Showing 81 - 100 of 180
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)