Exam 7: Introduction to Probability
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
If you draw one card at random from a deck of 10 cards numbered 1 through 10, inclusive, what is the probability that the number you draw is divisible by 9?
(Multiple Choice)
4.8/5  (26)
(26)
In a certain city, the Democratic, Republican, and Consumer parties have members of their parties on the city council. The probability of a member of this party winning in any election depends on the proportional membership of his/her party at the time of the election. The probabilities for all these parties winning are given by the following transition matrix P. Using the given transition matrix and assuming the initial-probability vector is 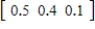 , find the probability vectors for the next four steps of the Markov chain. Round all numerical values in your answer to four decimal places.
, find the probability vectors for the next four steps of the Markov chain. Round all numerical values in your answer to four decimal places. 
(Multiple Choice)
4.9/5  (34)
(34)
Each of urns I and II has 2 red balls, 4 white balls, and 4 green balls. Urn III has 2 red balls, 5 white balls, and 3 green balls. An urn is selected at random and a ball is drawn. If the ball is green G, find the probability that urn III was selected.
(Multiple Choice)
4.8/5  (35)
(35)
Each computer component that the Peggos Company produces is tested twice before it is shipped. There is a 0.7 probability that a defective component will be so identified by the first test and a 0.8 probability that it will be identified as being defective by the second test. What is the probability that a defective component will not be identified as defective before it is shipped?
(Multiple Choice)
4.9/5  (34)
(34)
Three balls are drawn, without replacement, from a bag containing 8 red balls and 6 white balls. Construct a probability tree to determine the probability that the third ball drawn is red R.
(Multiple Choice)
4.9/5  (39)
(39)
A bag contains 5 white balls and 5 red balls. Construct a probability tree to determine the probability that if 2 balls are drawn, with replacement, the first ball is red R or the second is white W.
(Multiple Choice)
5.0/5  (33)
(33)
A small town has 8000 adult males and 6500 adult females. A sociologist conducted a survey and found that 40% of the males and 30% of the females drink heavily. An adult is selected at random from the town. What is the probability, rounded to four decimal places, that the person is male M, if it is known that the person drinks heavily DH?
(Multiple Choice)
4.9/5  (38)
(38)
Suppose that five of the eight students running for class officers (president, vice president, secretary, and treasurer) have grade-point averages (GPAs) above 3.0. If the officers are selected at random, what is the probability that all four officers will be students with GPAs above 3.0?
(Multiple Choice)
4.9/5  (35)
(35)
What is the probability of being dealt a poker hand of 5 cards containing exactly 5 cards of the same suit? Round your answer to six decimal places.
(Multiple Choice)
4.8/5  (28)
(28)
A bag contains 7 white balls and 3 red balls. Construct a probability tree to determine the probability that if 2 balls are drawn, with replacement, both balls are red R.
(Multiple Choice)
4.9/5  (33)
(33)
From a deck of 52 ordinary playing cards, one card is drawn. What is the probability that it is a spade(S)?
(Multiple Choice)
4.7/5  (33)
(33)
A ball is drawn from a bag containing 14 red balls numbered 1-14 and 11 white balls numbered 15-25. What is the probability that the ball is red R or even-numbered E?
(Multiple Choice)
4.9/5  (35)
(35)
One ball is drawn at random from a bag containing 6 red R balls and 10 white W balls. What is the probability that the ball is red or white?
(Multiple Choice)
4.8/5  (36)
(36)
Of 100 students, 26 can speak French F, 33 can speak German G, and 16 can speak both French and German. If a student is picked at random, what is the probability that he or she can speak French or German?
(Multiple Choice)
4.8/5  (38)
(38)
A bag contains 9 white balls and 5 red balls. Three balls are drawn, without replacement, from the bag. Construct a probability tree to determine the probability that all three balls are white W.
(Multiple Choice)
4.8/5  (32)
(32)
A bag contains 7 red balls numbered 1-7 and 15 white balls numbered 8-22. One ball is drawn from the bag. What is the probability that the ball is red R, given that the ball is even-numbered E?
(Multiple Choice)
4.8/5  (37)
(37)
A ball is drawn from a bag containing 8 red balls numbered 1-8 and 7 white balls numbered 9-15. What is the probability that the ball is neither red R nor even-numbered E?
(Multiple Choice)
4.9/5  (37)
(37)
A car dealer has 15 different cars that he would like to display, but he has room to display only 5. Suppose 9 of the cars are the same color, with the remaining 6 having different colors that are distinct from each other. If the dealer tells a salesperson to display any 5 cars, what is the probability that all 5 cars will be the same color?
(Multiple Choice)
4.8/5  (29)
(29)
An ordinary die is tossed. What is the probability of getting an even number or a number divisible by 6?
(Multiple Choice)
5.0/5  (28)
(28)
Showing 101 - 120 of 180
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)