Exam 13: Definite Integrals - Techniques
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
In an effort to make the distribution of income more nearly equal, the government of a country passes a tax law that changes the Lorenz curve from 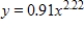 for 2004 to
for 2004 to 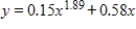 for 2005. Find the Gini coefficient of income for both years. Round your answer to six decimal places.
for 2005. Find the Gini coefficient of income for both years. Round your answer to six decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
Suppose that the profit from a machine's production can be considered as a continuous income stream with annual rate of flow at time t given by 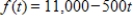 (dollars per year). If money is worth 14%, compounded continuously, find the present value of this stream over the next 5 years. Round your answer to the nearest dollar.
(dollars per year). If money is worth 14%, compounded continuously, find the present value of this stream over the next 5 years. Round your answer to the nearest dollar.
(Multiple Choice)
4.8/5  (39)
(39)
If the marginal cost function for x units of a product is 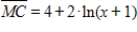 dollars per unit, and if the fixed cost is $120, find the total cost function.
dollars per unit, and if the fixed cost is $120, find the total cost function.
(Multiple Choice)
4.9/5  (33)
(33)
The probability density function for the life span of an electronics part is 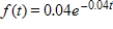 where t is the number of months in service. Find the probability that any given part of this type lasts longer than 18 months. Round your answer to three decimal places.
where t is the number of months in service. Find the probability that any given part of this type lasts longer than 18 months. Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (36)
(36)
A continuous income stream has an annual rate of flow at time t given by 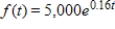 (dollars per year). Find the present value of this income stream for the next 9 years, if the money is worth 4% compounded continuously. Round to the nearest dollar.
(dollars per year). Find the present value of this income stream for the next 9 years, if the money is worth 4% compounded continuously. Round to the nearest dollar.
(Multiple Choice)
4.8/5  (39)
(39)
If the supply function for a commodity is 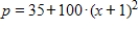 where p is in millions of dollars and x is the number of thousands of units. What is the producer's surplus at
where p is in millions of dollars and x is the number of thousands of units. What is the producer's surplus at 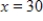 ? Round your answer to the nearest million dollars.
? Round your answer to the nearest million dollars.
(Multiple Choice)
4.7/5  (39)
(39)
Suppose that the rate at which a nuclear power plant produces radioactive waste is proportional to the number of years it has been operating, according to 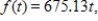 in pounds per year. Suppose also that the waste decays exponentially at a rate of 6% per year. Then the amount of radioactive waste that will accumulate in b years is given by
in pounds per year. Suppose also that the waste decays exponentially at a rate of 6% per year. Then the amount of radioactive waste that will accumulate in b years is given by 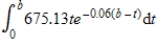 and this integral evaluates to
and this integral evaluates to 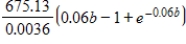 . How much waste will accumulate in the long run? Take the limit as
. How much waste will accumulate in the long run? Take the limit as 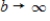 in the integral evaluated. Round your answer to the nearest pound, if it exists.
in the integral evaluated. Round your answer to the nearest pound, if it exists.
(Multiple Choice)
4.8/5  (38)
(38)
Find the area of the shaded region for the graph given below. 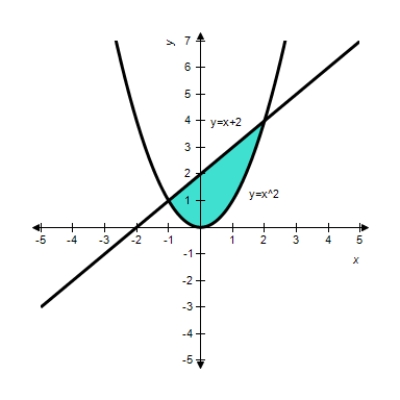
(Multiple Choice)
4.8/5  (42)
(42)
Use the Trapezoidal Rule to approximate 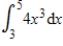 with n = 6. Round your answer to two decimal places.
with n = 6. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (39)
(39)
Determine the most appropriate method or integral formula for evaluating the given integral. Next, evaluate the integral.
I. Integration by parts
II. 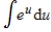 III.
III. 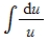 IV.
IV. 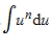
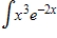
(Multiple Choice)
4.9/5  (39)
(39)
Assume that the tax burden per capita (in dollars) for selected years from 1950 to 2002 can be modeled by 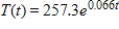 where
where 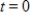 represents 1950. If the model remains valid, find the predicted average federal tax burden per capita from 2000 to 2010. Round your answer to the nearest dollar.
represents 1950. If the model remains valid, find the predicted average federal tax burden per capita from 2000 to 2010. Round your answer to the nearest dollar.
(Multiple Choice)
4.7/5  (37)
(37)
Evaluate the improper integral if it converges, or state that it diverges. 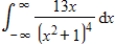
(Multiple Choice)
4.7/5  (41)
(41)
Showing 41 - 60 of 370
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)