Exam 13: Definite Integrals - Techniques
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
Evaluate the given integral with the Fundamental Theorem of Calculus 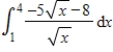 .
.
(Multiple Choice)
4.9/5  (30)
(30)
The demand function for a certain product is 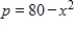 and the supply function is
and the supply function is 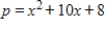 where p is in millions of dollars and x is the number of thousands of units. Find the equilibrium point (x, p) and the consumer's surplus there. Round your answer to the nearest million dollars, where applicable.
where p is in millions of dollars and x is the number of thousands of units. Find the equilibrium point (x, p) and the consumer's surplus there. Round your answer to the nearest million dollars, where applicable.
(Multiple Choice)
4.8/5  (33)
(33)
A small brewery considers the output of its bottling machine as a continuous income stream with an annual rate of flow at time t given by 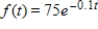 in thousands of dollars per year. Find the income from this stream for the next 30 years. Round your answer to the nearest dollar.
in thousands of dollars per year. Find the income from this stream for the next 30 years. Round your answer to the nearest dollar.
(Multiple Choice)
4.9/5  (41)
(41)
Suppose that a printing firm considers the production of its presses as a continuous income stream. If the annual rate of flow at time t is given by 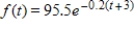 in thousands of dollars per year, and if money is worth 7% compounded continuously, find the present value and future value of the presses over the next 10 years. Round your answer to the nearest dollar.
in thousands of dollars per year, and if money is worth 7% compounded continuously, find the present value and future value of the presses over the next 10 years. Round your answer to the nearest dollar.
(Multiple Choice)
4.8/5  (43)
(43)
Suppose the rate of production of a new line of products is given by 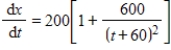 where x is the number of items produced and t is the number of weeks the products have been in production. How many units were produced in the first 3 weeks? Round your answer to the nearest unit produced.
where x is the number of items produced and t is the number of weeks the products have been in production. How many units were produced in the first 3 weeks? Round your answer to the nearest unit produced.
(Multiple Choice)
4.8/5  (34)
(34)
The rate of depreciation of a building is given by 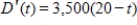 dollars per year,
dollars per year, 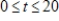 . Use the definite integral to find the total depreciation over the first 20 years.
. Use the definite integral to find the total depreciation over the first 20 years.
(Multiple Choice)
4.8/5  (33)
(33)
The Lorenz curve for the income distribution in a certain country in 2005 is given by 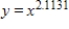 . Find the Gini coefficient of income for 2005 for this country. Round your answer to four decimal places.
. Find the Gini coefficient of income for 2005 for this country. Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
The demand function for a product is 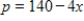 , where p is the number of dollars and x is the number of units. If the equilibrium price is $40, what is the consumer's surplus?
, where p is the number of dollars and x is the number of units. If the equilibrium price is $40, what is the consumer's surplus?
(Multiple Choice)
4.9/5  (29)
(29)
Suppose in a small city the response time t (in minutes) of the fire company is given by the probability density function 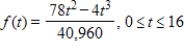 . For a fire chosen at random, find the probability that the response time is 10 minutes or less. Round your answer to three decimal places.
. For a fire chosen at random, find the probability that the response time is 10 minutes or less. Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (39)
(39)
Find the producer's surplus for a product with demand function 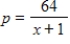 and supply function
and supply function 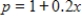 where p is in millions of dollars and x is the number of thousands of units. Round your answer to one decimal place.
where p is in millions of dollars and x is the number of thousands of units. Round your answer to one decimal place.
(Multiple Choice)
4.9/5  (42)
(42)
Evaluate the improper integral if it converges, or state that it diverges. 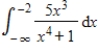
(Multiple Choice)
4.9/5  (33)
(33)
Find the producer's surplus for a product if its demand function is 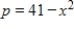 and its supply function is
and its supply function is 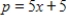 where p is in millions of dollars and x is the number of thousands of units. Round your answer to the nearest million dollars.
where p is in millions of dollars and x is the number of thousands of units. Round your answer to the nearest million dollars.
(Multiple Choice)
4.9/5  (44)
(44)
The supply function for a good is 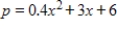 , where p is the number of dollars and x is the number of units. If the equilibrium price is $27 what is the producer's surplus at the equilibrium price? Round to the nearest cent.
, where p is the number of dollars and x is the number of units. If the equilibrium price is $27 what is the producer's surplus at the equilibrium price? Round to the nearest cent.
(Multiple Choice)
4.9/5  (41)
(41)
Evaluate the improper integral if it converges, or state that it diverges. 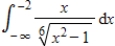
(Multiple Choice)
4.7/5  (43)
(43)
Consider the following supply and demand schedules, with p in dollars and x as the number of units. 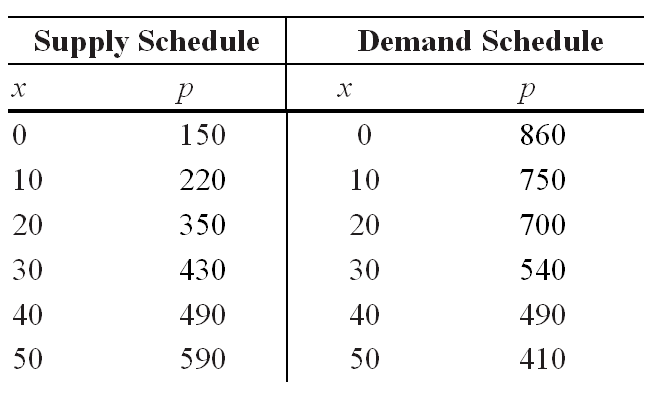 Use Simpson's Rule to approximate the producer's surplus at market equilibrium to 2 decimal places. Note that market equilibrium can be found from the tables.
Use Simpson's Rule to approximate the producer's surplus at market equilibrium to 2 decimal places. Note that market equilibrium can be found from the tables.
(Multiple Choice)
4.8/5  (40)
(40)
A transmission repair firm that wants to offer a lifetime warranty on its repairs has determined that the probability density function for transmission failure after repair is 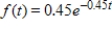 , where t is the number of months after repair. What is the probability that a transmission chosen at random will last more than 4 months? Round to 3 decimal places.
, where t is the number of months after repair. What is the probability that a transmission chosen at random will last more than 4 months? Round to 3 decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
The demand function for a product is 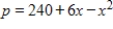 , and the supply function for it is
, and the supply function for it is 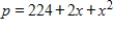 , where p is the number of dollars and x is the number of units. If the equilibrium price is $248 what is the producer's surplus at the equilibrium price? Round to the nearest cent.
, where p is the number of dollars and x is the number of units. If the equilibrium price is $248 what is the producer's surplus at the equilibrium price? Round to the nearest cent.
(Multiple Choice)
5.0/5  (42)
(42)
Showing 121 - 140 of 370
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)