Exam 13: Definite Integrals - Techniques
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
A transmission repair firm that wants to offer a lifetime warranty on its repairs has determined that the probability density function for transmission failure after repair is 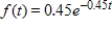 , where t is the number of months after repair. What is the probability that a transmission chosen at random will last more than 4 months? Round to 3 decimal places.
, where t is the number of months after repair. What is the probability that a transmission chosen at random will last more than 4 months? Round to 3 decimal places.
(Multiple Choice)
4.8/5  (37)
(37)
Evaluate the improper integral if it converges, or state that it diverges.
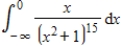
(Multiple Choice)
4.8/5  (36)
(36)
The demand function for a certain product is 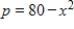 and the supply function is
and the supply function is 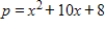 where p is in millions of dollars and x is the number of thousands of units. Find the equilibrium point (x, p) and the consumer's surplus there. Round your answer to the nearest million dollars, where applicable.
where p is in millions of dollars and x is the number of thousands of units. Find the equilibrium point (x, p) and the consumer's surplus there. Round your answer to the nearest million dollars, where applicable.
(Multiple Choice)
4.8/5  (41)
(41)
The production from a particular assembly line is considered a continuous income stream with annual rate of flow given by 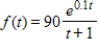 (in thousands of dollars per year). Use Simpson's Rule with n = 4 to approximate the total income to 2 decimal places over the first 2 years, given by
(in thousands of dollars per year). Use Simpson's Rule with n = 4 to approximate the total income to 2 decimal places over the first 2 years, given by 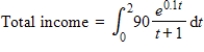 .
.
(Multiple Choice)
5.0/5  (40)
(40)
Suppose that the demand for q units of a certain product at p per unit is given by 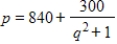 . Use Simpson's Rule with n = 6 to approximate the average price as demand ranges from 3 to 8 items to the nearest cent.
. Use Simpson's Rule with n = 6 to approximate the average price as demand ranges from 3 to 8 items to the nearest cent.
(Multiple Choice)
4.9/5  (44)
(44)
Use integration by parts to evaluate 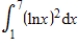 . Note that evaluation may require integration by parts more than once.
. Note that evaluation may require integration by parts more than once.
(Multiple Choice)
4.8/5  (35)
(35)
Use formulas or numerical integration with a graphing calculator or computer to evaluate the given definite integral. Round answer to three decimal places. 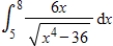
(Multiple Choice)
4.7/5  (39)
(39)
Assume that a store finds that its sales revenue changes at a rate given by 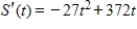 dollars per day, where t is the number of days after an advertising campaign ends and
dollars per day, where t is the number of days after an advertising campaign ends and 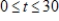 . Find the total sales for the second week after the campaign ends
. Find the total sales for the second week after the campaign ends 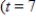 to
to 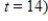 .
.
(Multiple Choice)
4.8/5  (50)
(50)
Approximate the area under the curve over the specified interval by using the indicated number of subintervals (or rectangles) and evaluating the function at the right-hand endpoints of the subintervals. Compute the approximate area using up to four decimal places as needed. 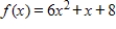 from
from 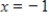 to
to 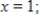
 subintervals.
subintervals.
(Multiple Choice)
4.9/5  (42)
(42)
Use Simpson's Rule to approximate 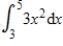 with n = 6. Round your answer to two decimal places.
with n = 6. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (36)
(36)
Use the Trapezoidal Rule to approximate 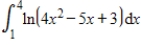 with n = 4. Round your answer to 3 decimal places.
with n = 4. Round your answer to 3 decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
Use integration by parts to evaluate the integral 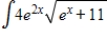 . Note that evaluation may require integration by parts more than once.
. Note that evaluation may require integration by parts more than once.
(Multiple Choice)
4.9/5  (37)
(37)
Equations are given whose graphs enclose a region. Find the area of the region. 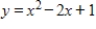 ,
, 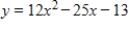 ,
, 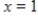 and
and 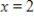
(Multiple Choice)
4.9/5  (39)
(39)
Showing 141 - 160 of 370
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)