Exam 13: Definite Integrals - Techniques
Exam 1: Linear Equations and Functions245 Questions
Exam 2: Quadratic and Other Special Functions120 Questions
Exam 3: Matrices230 Questions
Exam 4: Inequalities and Linear Programming119 Questions
Exam 5: Exponential and Logarithmic Functions109 Questions
Exam 6: Mathematics of Finance131 Questions
Exam 7: Introduction to Probability180 Questions
Exam 8: Further Topics in Probability and Data Description114 Questions
Exam 9: Derivatives249 Questions
Exam 10: Derivatives172 Questions
Exam 11: Derivatives Continued139 Questions
Exam 12: Indefinite Integrals120 Questions
Exam 13: Definite Integrals - Techniques370 Questions
Exam 13: A: Definite Integrals - Techniques370 Questions
Exam 14: Functions of Two or More Variables122 Questions
Exam 15: Algebraic Concepts 240 Questions
Exam 15: Algebraic Concepts 374 Questions
Exam 15: Algebraic Concepts 496 Questions
Exam 15: Algebraic Concepts 599 Questions
Select questions type
The total cost function for a product is 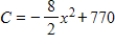 , and the demand function is
, and the demand function is 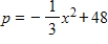 , where p is the number of dollars and x is the number of units. Find the consumer's surplus at the point where the product has maximum profit. Round to the nearest cent.
, where p is the number of dollars and x is the number of units. Find the consumer's surplus at the point where the product has maximum profit. Round to the nearest cent.
(Multiple Choice)
4.8/5  (41)
(41)
The graph in the following figure gives the times that it takes a vehicle to reach speeds from 0 mph to 25 mph, in increments of 5 mph, with a curve connecting them. Count the squares under the curve to estimate this distance. Estimate the distance traveled by the vehicle in 14 seconds, to a speed of 25 mph. (Be careful with time units.) 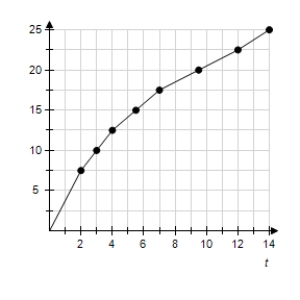
(Multiple Choice)
4.9/5  (32)
(32)
Determine the most appropriate method or integral formula for evaluating the given integral. Next, evaluate the integral.
I. Integration by parts
II. 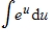 III.
III. 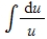 IV.
IV. 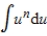
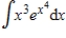
(Multiple Choice)
5.0/5  (42)
(42)
Use the sum formulas to find the value of the sum that follows. 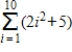
(Multiple Choice)
4.9/5  (38)
(38)
The following table shows the rate of oil consumption (in thousands of barrels per year) by a certain city. Estimate the total consumption of oil by the city from 1999 -2004 by using 5 equal subdivisions and left-hand endpoints to estimate the area under the graph that corresponds to the table from 1999 to 2004. 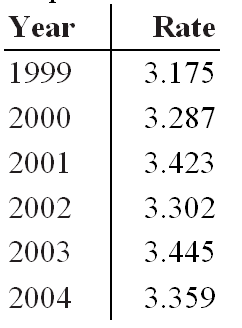
(Multiple Choice)
5.0/5  (35)
(35)
Use the function 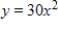 from
from 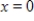 to
to 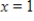 and n equal subintervals with the function evaluated at the right-hand endpoints of each subinterval. Let the sum of the areas of the rectangles be S. Find
and n equal subintervals with the function evaluated at the right-hand endpoints of each subinterval. Let the sum of the areas of the rectangles be S. Find 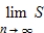 by using the formula for the sum of the areas of the n rectangles.
by using the formula for the sum of the areas of the n rectangles.
(Multiple Choice)
4.9/5  (34)
(34)
The demand function for a certain product is given by 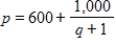 , where p is the price and q is the number of units demanded. Find the average price as demand ranges from 35 to 81 units. Round your answer to the nearest penny.
, where p is the price and q is the number of units demanded. Find the average price as demand ranges from 35 to 81 units. Round your answer to the nearest penny.
(Multiple Choice)
4.9/5  (41)
(41)
Use the sum formulas to find the value of the sum that follows. 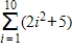
(Multiple Choice)
4.9/5  (28)
(28)
Suppose that a vending machine service company models its income by assuming that money flows continuously into the machines, with the annual rate of flow given by 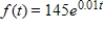 in thousands of dollars per year. Find the total income from the machines predicted by the model over the first 5 years. Round your answer to the nearest thousand dollars.
in thousands of dollars per year. Find the total income from the machines predicted by the model over the first 5 years. Round your answer to the nearest thousand dollars.
(Multiple Choice)
4.8/5  (37)
(37)
If the demand function for a product is 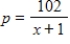 and the supply function is
and the supply function is 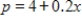 where p is in millions of dollars and x is the number of thousands of units. Find the consumer's surplus. Round your answer to the nearest million dollars.
where p is in millions of dollars and x is the number of thousands of units. Find the consumer's surplus. Round your answer to the nearest million dollars.
(Multiple Choice)
4.9/5  (39)
(39)
Use Simpson's Rule to approximate 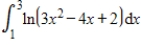 with n = 6. Round your answer to 3 decimal places.
with n = 6. Round your answer to 3 decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
The average life for a particular brand of car battery is given by the following probability density function where t is in years. 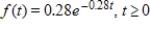 Find the probability that a battery chosen at random lasts between 2 and 7 years. Round your answer to two decimal places.
Find the probability that a battery chosen at random lasts between 2 and 7 years. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (33)
(33)
The cost of producing x units of a certain item is 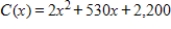 Find the average value of the cost function C(x) over the interval from 0 to 1,000. Round answer to nearest penny.
Find the average value of the cost function C(x) over the interval from 0 to 1,000. Round answer to nearest penny.
(Multiple Choice)
4.8/5  (29)
(29)
Use Simpson's Rule to approximate 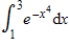 with n = 4. Round your answer to 3 decimal places.
with n = 4. Round your answer to 3 decimal places.
(Multiple Choice)
4.7/5  (32)
(32)
Showing 101 - 120 of 370
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)