Exam 17: Second-Order Differential Equations
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
The solution of the initial-value problem 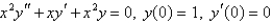 is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function.
is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function.
(Multiple Choice)
4.8/5  (51)
(51)
Solve the differential equation using the method of variation of parameters. 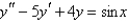
(Essay)
4.9/5  (37)
(37)
A spring with a 3-kg mass is held stretched 0.9 m beyond its natural length by a force of 30 N. If the spring begins at its equilibrium position but a push gives it an initial velocity of 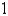 m/s, find the position x(t) of the mass after t seconds.
m/s, find the position x(t) of the mass after t seconds.
(Multiple Choice)
4.8/5  (37)
(37)
Solve the differential equation using the method of undetermined coefficients. 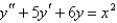
(Multiple Choice)
4.9/5  (42)
(42)
Solve the differential equation using the method of variation of parameters. 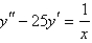
(Essay)
4.8/5  (27)
(27)
A series circuit consists of a resistor 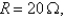 an inductor with L =
an inductor with L = 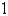 H, a capacitor with
C =
H, a capacitor with
C = 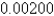 F, and a
F, and a 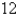 -V battery. If the initial charge and current are both 0, find the charge Q(t) at time t.
-V battery. If the initial charge and current are both 0, find the charge Q(t) at time t.
(Essay)
4.9/5  (36)
(36)
A spring with a mass of 2 kg has damping constant 14, and a force of 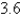 N is required to keep the spring stretched
N is required to keep the spring stretched 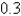 m beyond its natural length. The spring is stretched 1m beyond its natural length and then released with zero velocity. Find the position x(t) of the mass at any time t.
m beyond its natural length. The spring is stretched 1m beyond its natural length and then released with zero velocity. Find the position x(t) of the mass at any time t.
(Essay)
4.8/5  (42)
(42)
Solve the initial-value problem using the method of undetermined coefficients. 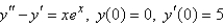
(Essay)
4.9/5  (39)
(39)
Find a trial solution for the method of undetermined coefficients. Do not determine the coefficients. 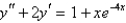
(Multiple Choice)
5.0/5  (40)
(40)
Showing 41 - 60 of 63
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)