Exam 11: Infinite Sequences and Series
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Determine whether the given series converges or diverges. If it converges, find its sum. 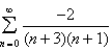
(Essay)
4.9/5  (39)
(39)
Determine whether the sequence is increasing, decreasing, or not monotonic. Is the sequence bounded? 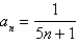
(Multiple Choice)
4.9/5  (42)
(42)
Determine whether the sequence defined as follows is convergent or divergent. 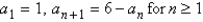
(Short Answer)
4.8/5  (37)
(37)
Determine whether the sequence defined by 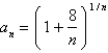 converges or diverges. If it converges, find its limit.
converges or diverges. If it converges, find its limit.
(Short Answer)
4.7/5  (34)
(34)
Find an expression for the 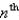 term of the sequence. (Assume that the pattern continues.)
term of the sequence. (Assume that the pattern continues.) 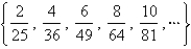
(Essay)
4.8/5  (38)
(38)
Given the series 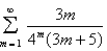 estimate the error in using the partial sum
estimate the error in using the partial sum  by comparison with the series
by comparison with the series 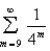 .
.
(Multiple Choice)
4.7/5  (46)
(46)
Determine whether the sequence defined by 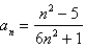 converges or diverges. If it converges, find its limit.
converges or diverges. If it converges, find its limit.
(Multiple Choice)
4.8/5  (37)
(37)
Find the Maclaurin series for 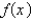 using the definition of a Maclaurin serires.
using the definition of a Maclaurin serires. 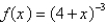
(Essay)
4.8/5  (39)
(39)
Write the partial sum of the converging series which represent the decimal number 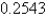 .
.
(Essay)
4.8/5  (33)
(33)
Let 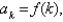 where f is a continuous, positive, and decreasing function on
where f is a continuous, positive, and decreasing function on 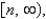 and suppose that
and suppose that 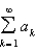 is convergent. Defining
is convergent. Defining 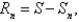 where
where 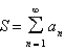 and
and 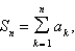 we have that
we have that 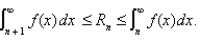 Find the maximum error if the sum of the series
Find the maximum error if the sum of the series 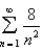 is approximated by
is approximated by 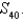
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the given series is convergent or divergent. 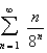
(Short Answer)
4.8/5  (43)
(43)
Find the Maclaurin series for f (x) using the definition of the Maclaurin series. 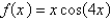
(Multiple Choice)
4.8/5  (35)
(35)
Use the Integral Test to determine whether the series is convergent or divergent. 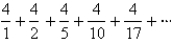
(Short Answer)
4.7/5  (37)
(37)
Showing 121 - 140 of 158
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)