Exam 10: Parametric Equations and Polar Coordinates
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Sketch the parametric curve and eliminate the parameter to find the Cartesian equation of the curve. 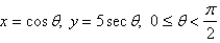
(Essay)
4.9/5  (41)
(41)
Find the polar equation for the curve represented by the given Cartesian equation. 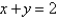
(Multiple Choice)
4.8/5  (34)
(34)
Find an equation of the hyperbola centered at the origin that satisfies the given condition. Vertices: (± 4, 0), asymptotes: y = ± 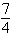 x
x
(Multiple Choice)
4.8/5  (38)
(38)
The planet Mercury travels in an elliptical orbit with eccentricity 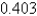 . Its minimum distance from the Sun is
. Its minimum distance from the Sun is 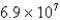 km. If the perihelion distance from a planet to the Sun is
km. If the perihelion distance from a planet to the Sun is 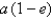 and the aphelion distance is
and the aphelion distance is 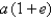 , find the maximum distance (in km) from Mercury to the Sun.
, find the maximum distance (in km) from Mercury to the Sun.
(Multiple Choice)
4.9/5  (31)
(31)
Describe the motion of a particle with position 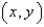 as t varies in the given interval
as t varies in the given interval 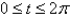 .
. 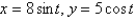
(Multiple Choice)
4.9/5  (43)
(43)
Consider the polar equation 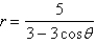 .
(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.
.
(a) Find the eccentricity and an equation of the directrix of the conic.
(b) Identify the conic.
(c) Sketch the curve.
(Essay)
4.9/5  (38)
(38)
Use a graph to estimate the values of  for which the curves
for which the curves 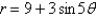 and
and 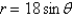 intersect. Round your answer to two decimal places.
intersect. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (37)
(37)
Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. 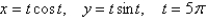
(Essay)
4.9/5  (47)
(47)
Find the exact area of the surface obtained by rotating the given curve about the x-axis. 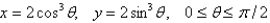
(Multiple Choice)
4.9/5  (40)
(40)
Find an equation of the ellipse that satisfies the given conditions. Foci: (0, ± 1), vertices (0, ± 6)
(Multiple Choice)
4.9/5  (41)
(41)
The orbit of Hale-Bopp comet, discovered in 1995, is an ellipse with eccentricity ![The orbit of Hale-Bopp comet, discovered in 1995, is an ellipse with eccentricity and one focus at the Sun. The length of its major axis is AU. [An astronomical unit (AU) is the mean distance between Earth and the Sun, about 93 million miles.] Find the maximum distance from the comet to the Sun. (The perihelion distance from a planet to the Sun is and the aphelion distance is .) Find the answer in AU and round to the nearest hundredth.](https://storage.examlex.com/TB5971/11eaa3e5_5518_d38a_9f8f_1d3ec6b16e0c_TB5971_11.jpg) and one focus at the Sun. The length of its major axis is
and one focus at the Sun. The length of its major axis is ![The orbit of Hale-Bopp comet, discovered in 1995, is an ellipse with eccentricity and one focus at the Sun. The length of its major axis is AU. [An astronomical unit (AU) is the mean distance between Earth and the Sun, about 93 million miles.] Find the maximum distance from the comet to the Sun. (The perihelion distance from a planet to the Sun is and the aphelion distance is .) Find the answer in AU and round to the nearest hundredth.](https://storage.examlex.com/TB5971/11eaa3e5_5518_d38b_9f8f_dd27d447a3e6_TB5971_11.jpg) AU. [An astronomical unit (AU) is the mean distance between Earth and the Sun, about 93 million miles.] Find the maximum distance from the comet to the Sun. (The perihelion distance from a planet to the Sun is
AU. [An astronomical unit (AU) is the mean distance between Earth and the Sun, about 93 million miles.] Find the maximum distance from the comet to the Sun. (The perihelion distance from a planet to the Sun is ![The orbit of Hale-Bopp comet, discovered in 1995, is an ellipse with eccentricity and one focus at the Sun. The length of its major axis is AU. [An astronomical unit (AU) is the mean distance between Earth and the Sun, about 93 million miles.] Find the maximum distance from the comet to the Sun. (The perihelion distance from a planet to the Sun is and the aphelion distance is .) Find the answer in AU and round to the nearest hundredth.](https://storage.examlex.com/TB5971/11eaa3e5_5518_d38c_9f8f_417b819c71c5_TB5971_11.jpg) and the aphelion distance is
and the aphelion distance is ![The orbit of Hale-Bopp comet, discovered in 1995, is an ellipse with eccentricity and one focus at the Sun. The length of its major axis is AU. [An astronomical unit (AU) is the mean distance between Earth and the Sun, about 93 million miles.] Find the maximum distance from the comet to the Sun. (The perihelion distance from a planet to the Sun is and the aphelion distance is .) Find the answer in AU and round to the nearest hundredth.](https://storage.examlex.com/TB5971/11eaa3e5_5518_d38d_9f8f_ef3714f8820c_TB5971_11.jpg) .) Find the answer in AU and round to the nearest hundredth.
.) Find the answer in AU and round to the nearest hundredth.
(Multiple Choice)
4.9/5  (32)
(32)
A cow is tied to a silo with radius 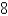 by a rope just long enough to reach the opposite side of the silo. Find the area available for grazing by the cow. Round the answer to the nearest hundredth.
by a rope just long enough to reach the opposite side of the silo. Find the area available for grazing by the cow. Round the answer to the nearest hundredth. 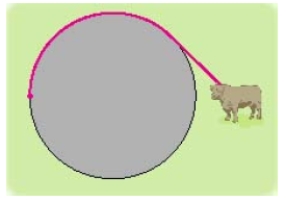
(Essay)
4.8/5  (40)
(40)
Showing 21 - 40 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)