Exam 5: Discrete Probability Distributions
Exam 1: Statistics and Data68 Questions
Exam 2: Tabular and Graphical Methods99 Questions
Exam 3: Numerical Descriptive Measures123 Questions
Exam 4: Basic Probability Concepts107 Questions
Exam 5: Discrete Probability Distributions118 Questions
Exam 6: Continuous Probability Distributions114 Questions
Exam 7: Sampling and Sampling Distributions110 Questions
Exam 8: Interval Estimation111 Questions
Exam 9: Hypothesis Testing111 Questions
Exam 10: Statistical Inference Concerning Two Populations104 Questions
Exam 11: Statistical Inference Concerning Variance96 Questions
Exam 12: Chi-Square Tests100 Questions
Exam 13: Analysis of Variance89 Questions
Exam 14: Regression Analysis116 Questions
Exam 15: Inference With Regression Models117 Questions
Exam 16: Regression Models for Nonlinear Relationships95 Questions
Exam 17: Regression Models With Dummy Variables117 Questions
Exam 18: Time Series and Forecasting103 Questions
Exam 19: Returns, Index Numbers and Inflation98 Questions
Exam 20: Nonparametric Tests99 Questions
Select questions type
A roll of steel is manufactured on a processing line.The anticipated number of defects in a 10-foot segment of this roll is two.What is the probability of no defects in 10 feet of steel?
(Multiple Choice)
4.8/5  (33)
(33)
A risk-averse consumer may decline a risky prospect even if it offers a positive expected value.
(True/False)
4.8/5  (29)
(29)
You have inherited a lottery ticket worth $10,000.You have a 0.25 chance of winning the $10,000 and a 0.75 chance of winning $0.You have an opportunity to sell the lottery ticket for $2,500.What should you do if you are risk averse?
(Essay)
4.8/5  (36)
(36)
Exhibit 5-2.Consider the following cumulative distribution function for the discrete random variable X.  Refer to Exhibit 5-2.What is the probability that X is less than or equal to 2?
Refer to Exhibit 5-2.What is the probability that X is less than or equal to 2?
(Multiple Choice)
4.8/5  (36)
(36)
Given two random variables X and Y,the expected value of their sum, 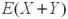 ,is equal to the sum of their individual expected values,
,is equal to the sum of their individual expected values, 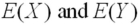 .
.
(True/False)
4.8/5  (38)
(38)
Assume that the mean success rate of a Poisson process is six successes per hour.
A)Find the expected number of successes in a 40-minute period.
B)Find the expected number of successes in a three-hour period.
C)Find the probability of at least two successes in a 30-minute period.
(Essay)
4.9/5  (28)
(28)
Exhibit 5-2.Consider the following cumulative distribution function for the discrete random variable X.  Refer to Exhibit 5-2.What is the probability that X is greater than 2?
Refer to Exhibit 5-2.What is the probability that X is greater than 2?
(Multiple Choice)
4.9/5  (33)
(33)
Exhibit 5-9.On a particular production line,the likelihood that a light bulb is defective is 5%.Ten light bulbs are randomly selected. Refer to Exhibit 5-9.What is the probability that two light bulbs will be defective?
(Multiple Choice)
4.9/5  (32)
(32)
Exhibit 5-6.The number of cars sold by a car salesman during each of the last 25 weeks is the following: 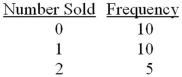 Refer to Exhibit 5-6.What is the expected number of cars sold by the salesman during a week?
Refer to Exhibit 5-6.What is the expected number of cars sold by the salesman during a week?
(Multiple Choice)
4.7/5  (31)
(31)
Exhibit 5-10.According to a study by the Centers for Disease Control and Prevention,about 33% of U.S.births are Caesarean deliveries (National Vital Statistics Report,Volume 60,Number 2,November 2011).Suppose seven expectant mothers are randomly selected. Refer to Exhibit 5-10.What is the probability that 2 of the expectant mothers will have a Caesarean delivery?
(Multiple Choice)
4.8/5  (37)
(37)
A binomial random variable is defined as the number of successes achieved in n trials of a Bernoulli process.
(True/False)
4.8/5  (25)
(25)
Cars arrive randomly at a tollbooth at a rate of 20 cars per 10 minutes during rush hour.What is the probability that exactly five cars will arrive over a five-minute interval during rush hour?
(Multiple Choice)
4.8/5  (32)
(32)
Exhibit 5-5.The number of homes sold by a realtor during a month has the following probability distribution: 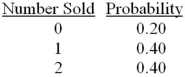 Refer to Exhibit 5-5.What is the standard deviation of the number of homes sold by the realtor during a month?
Refer to Exhibit 5-5.What is the standard deviation of the number of homes sold by the realtor during a month?
(Multiple Choice)
4.9/5  (25)
(25)
Which of the following can be represented by a continuous random variable?
(Multiple Choice)
4.9/5  (39)
(39)
A discrete random variable X may assume an (infinitely)uncountable number of distinct values.
(True/False)
4.9/5  (40)
(40)
Exhibit 5-16.According to geologists,the San Francisco Bay Area experiences five earthquakes with a magnitude of 6.5 or greater every 100 years. Refer to Exhibit 5-16.What is the probability that one or more earthquakes with a magnitude of 6.5 or greater will strike the San Francisco Bay Area in the next year?
(Multiple Choice)
4.8/5  (35)
(35)
George buys six lottery tickets for $2 each.In addition to the grand prize,there is a 20% chance that each lottery ticket gives a prize of $4.Assume that these tickets are not grand prize winners.
A)What is the probability that the tickets pay out more than George spent on them?
B)What is the probability that none of the tickets are winners?
C)What is the probability that at least one of the tickets is a winner?
(Essay)
4.8/5  (30)
(30)
A probability distribution of a continuous random variable X gives the probability that X takes on a particular value x,P(X = x).
(True/False)
4.8/5  (29)
(29)
Exhibit 5-9.On a particular production line,the likelihood that a light bulb is defective is 5%.Ten light bulbs are randomly selected. Refer to Exhibit 5-9.What are the mean and variance of the number of defective bulbs?
(Multiple Choice)
4.9/5  (43)
(43)
Exhibit 5-16.According to geologists,the San Francisco Bay Area experiences five earthquakes with a magnitude of 6.5 or greater every 100 years. Refer to Exhibit 5-16.What is the probability that no earthquakes with a magnitude of 6.5 or greater strike the San Francisco Bay Area in the next 40 years?
(Multiple Choice)
4.8/5  (40)
(40)
Showing 61 - 80 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)