Exam 4: Basic Probability Concepts
Exam 1: Statistics and Data68 Questions
Exam 2: Tabular and Graphical Methods99 Questions
Exam 3: Numerical Descriptive Measures123 Questions
Exam 4: Basic Probability Concepts107 Questions
Exam 5: Discrete Probability Distributions118 Questions
Exam 6: Continuous Probability Distributions114 Questions
Exam 7: Sampling and Sampling Distributions110 Questions
Exam 8: Interval Estimation111 Questions
Exam 9: Hypothesis Testing111 Questions
Exam 10: Statistical Inference Concerning Two Populations104 Questions
Exam 11: Statistical Inference Concerning Variance96 Questions
Exam 12: Chi-Square Tests100 Questions
Exam 13: Analysis of Variance89 Questions
Exam 14: Regression Analysis116 Questions
Exam 15: Inference With Regression Models117 Questions
Exam 16: Regression Models for Nonlinear Relationships95 Questions
Exam 17: Regression Models With Dummy Variables117 Questions
Exam 18: Time Series and Forecasting103 Questions
Exam 19: Returns, Index Numbers and Inflation98 Questions
Exam 20: Nonparametric Tests99 Questions
Select questions type
There are three unfilled seats on a small plane,but 10 people showed up to try to get one of those three unfilled seats.If the airline picks three people at random to get on the plane,what is the probability you and your two kids will get on the plane?
(Short Answer)
4.8/5  (38)
(38)
A pension plan gives you 12 possible funds to invest in,but you are only allowed to hold four at any given point in time.How many possible combinations of the 12 funds could you have in your portfolio?
(Short Answer)
4.8/5  (33)
(33)
The intersection of two events A and B,denoted by A ∩ B,is the event consisting of all outcomes that are in A and B
(True/False)
4.8/5  (31)
(31)
Exhibit 4-6.In January of 2012,the second stop for a Republican to get votes toward the presidential nomination was at the New Hampshire Primary.The following exhibit shows the votes several candidates received from registered Republicans and Independents.  Source: ABC News
Refer to Exhibit 4-6.What is the probability that a randomly selected voter voted for Ron Paul?
Source: ABC News
Refer to Exhibit 4-6.What is the probability that a randomly selected voter voted for Ron Paul?
(Short Answer)
4.7/5  (37)
(37)
The complement of an event A,within the sample space S,is the event consisting of ____________.
(Multiple Choice)
4.7/5  (36)
(36)
Romi,a production manager,is trying to improve the efficiency of his assembly line.He knows that the machine is set up correctly only 70% of the time.He also knows that if the machine is set up correctly,it will produce good parts 95% of the time,but if set up incorrectly,it will produce good parts only 40% of the time.Romi starts the machine and produces one part before he begins the production run.He finds the first part to be good.What is the revised probability that the machine was set up correctly?
(Multiple Choice)
4.8/5  (32)
(32)
An analyst believes the probability that U.S.stock returns exceed long-term corporate bond returns over a 5-year period is based on personal assessment.This type of probability is best characterized as a(n)___________.
(Multiple Choice)
4.8/5  (32)
(32)
Bayes' theorem uses the total probability rule to update the prior probability of an event that has not been affected by any new evidence.
(True/False)
4.9/5  (37)
(37)
The following table summarizes the ages of the 400 richest Americans.Suppose we select one of these individuals.Find the probability that the selected individual is at least 60 years old. 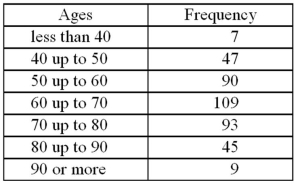
(Short Answer)
4.9/5  (40)
(40)
An experiment consists of rolling a fair die.Find the probability that we roll a 4 or a 6.
(Short Answer)
4.9/5  (32)
(32)
Bayes' theorem is used to update prior probabilities based on the arrival of new relevant information.
(True/False)
4.9/5  (46)
(46)
Restaurants in London,Paris,and New York want diners to experience eating in pitch darkness to heighten their senses of taste and smell (Vanity Fair,December 2011).Suppose 400 people were asked: "If given the opportunity,would you eat at one of these restaurants?" The accompanying contingency table,cross-classified by age,would be produced. 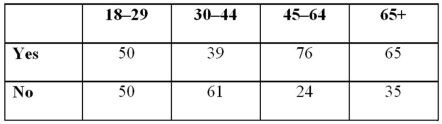 a.What is the probability that a respondent would eat at one of these restaurants?
B)What is the probability that a respondent would eat at one of these restaurants or is in the 30-44 age bracket?
C)Given that the respondent would eat at one of these restaurants,what is the probability that he/she is in the 30-44 age bracket?
D)Is whether a respondent would eat at one of these restaurants independent of one's age? Explain using probabilities.
a.What is the probability that a respondent would eat at one of these restaurants?
B)What is the probability that a respondent would eat at one of these restaurants or is in the 30-44 age bracket?
C)Given that the respondent would eat at one of these restaurants,what is the probability that he/she is in the 30-44 age bracket?
D)Is whether a respondent would eat at one of these restaurants independent of one's age? Explain using probabilities.
(Short Answer)
4.8/5  (30)
(30)
Exams are approaching and Helen is allocating time to studying for exams.She feels that with the appropriate amount of studying,she has an 80% chance of getting an A in Marketing.She also feels that she has a 60% chance of getting an A in Spanish with the appropriate amount of studying.Given the demands on her time,she feels that she has only a 45% chance of getting an A in both classes.What is the probability that Helen does not get an A in either class?
(Short Answer)
4.8/5  (33)
(33)
The likelihood of rain has been reported at 80% for next week.Find the odds for rain occurring.
(Short Answer)
4.7/5  (35)
(35)
Ryan is hoping to attend graduate school next year.Two of the schools he applied to are the University of Utah and Ohio State University.The probability he gets accepted to Utah given he got accepted to Ohio State is 0.75.The probability he gets accepted to Ohio State is 0.05.The probability he gets accepted to Utah is 0.10.What is the probability he gets accepted to Ohio State given he gets accepted to Utah?
(Short Answer)
4.8/5  (38)
(38)
Showing 41 - 60 of 107
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)