Exam 11: Waiting Line Models
Exam 1: Introduction53 Questions
Exam 2: An Introduction to Linear Programming56 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution44 Questions
Exam 4: Linear Programming Applications in Marketing, finance, and OM52 Questions
Exam 5: Advanced Linear Programming Applications39 Questions
Exam 6: Distribution and Network Models62 Questions
Exam 7: Integer Linear Programming52 Questions
Exam 8: Nonlinear Optimization Models45 Questions
Exam 9: Project Scheduling: Pertcpm60 Questions
Exam 10: Inventory Models60 Questions
Exam 11: Waiting Line Models56 Questions
Exam 12: Simulation53 Questions
Exam 13: Decision Analysis80 Questions
Exam 14: Multicriteria Decisions42 Questions
Exam 15: Time Series Analysis and Forecasting53 Questions
Exam 16: Markov Processes36 Questions
Exam 17: Linear Programming: Simplex Method45 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality32 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems39 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming41 Questions
Select questions type
Little's flow equations indicate that the relationship of L to Lq is the same as that of W to Wq.
(True/False)
4.8/5  (36)
(36)
Performance measures dealing with the number of units in line and the time spent waiting are called
(Multiple Choice)
4.8/5  (35)
(35)
When no limit is placed on how many units may seek service,the waiting line model
(Multiple Choice)
4.9/5  (33)
(33)
The total cost for a waiting line does NOT specifically depend on the
(Multiple Choice)
4.9/5  (39)
(39)
For many waiting line situations,the arrivals occur randomly and independently of other arrivals and it has been found that a good description of the arrival pattern is provided by a(n)
(Multiple Choice)
4.8/5  (24)
(24)
When blocked customers are cleared,an important decision is how many servers to provide.
(True/False)
4.8/5  (42)
(42)
The eight students in a seminar class must come to the professor's office to turn in a paper and give a five-minute oral summary.Assume there is a service rate of 10 per hour and adequate time is available for all.The arrival rate for each unit is five per hour.What is the probability there is no one in the office or waiting when you come?
(Short Answer)
4.9/5  (28)
(28)
Quick Clean Rooter cleans out clogged drains.Due to the competitive nature of the drain cleaning business,if a customer calls Quick Clean and finds the line busy,they immediately try another company and Quick Clean loses the business.Quick Clean management estimates that,on average,a customer tries to call Quick Clean every three minutes and the average time to take a service order is 200 seconds.The company wishes to hire enough operators so that at most 4% of its potential customers get the busy signal.
a.How many operators should be hired to meet this objective?
b.Given your answer to part (a),what is the probability that all the operators are idle?
(Essay)
5.0/5  (32)
(32)
In waiting line applications,the exponential probability distribution indicates that approximately 63% of the service times are less than the mean service time.
(True/False)
4.8/5  (30)
(30)
After the startup or transient period,a waiting system is in steady-state operation and considered to be the normal operation of the waiting line.
(True/False)
4.8/5  (30)
(30)
Operating characteristics formulas for the single-server queue do NOT require
(Multiple Choice)
4.9/5  (31)
(31)
If service time follows an exponential probability distribution,approximately 63% of the service times are less than the mean service time.
(True/False)
4.7/5  (43)
(43)
For a single-server waiting line,the utilization factor is the probability that an arriving unit must wait for service.
(True/False)
4.9/5  (42)
(42)
Before waiting lines can be analyzed economically,the arrivals' cost of waiting must be estimated.
(True/False)
4.9/5  (38)
(38)
Single-booth ticket sales at a theater are an example of which of the following queuing models?
(Multiple Choice)
4.9/5  (36)
(36)
The mean number of units that can be served per time period is called
(Multiple Choice)
4.8/5  (34)
(34)
The Grand Movie Theater has one box office clerk.On average,each customer that comes to see a movie can be sold a ticket at the rate of six per minute.For the theater's normal offerings of older movies,customers arrive at the rate of three per minute.Assume arrivals follow the Poisson distribution and service times follow the exponential distribution.
a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Grand has booked the Stars Wars Trilogy and expects more customers.From conversations with other theater owners,it estimates that the arrival rate will increase to 10 per minute.Output is supplied for two- and three-cashier systems.
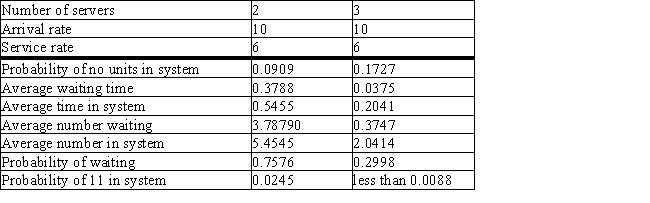
(Essay)
5.0/5  (43)
(43)
Showing 21 - 40 of 56
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)